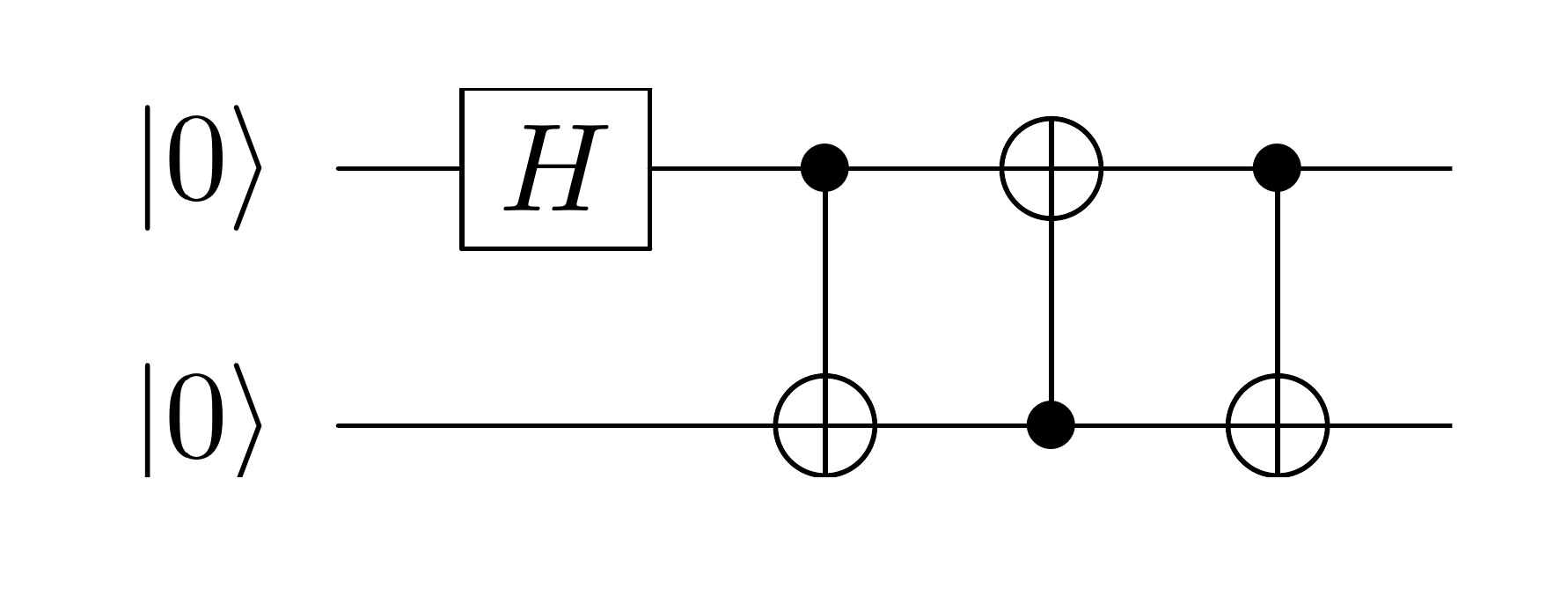
I made some supplementary material on cloning (copying), which works in the classical world but not in the quantum world.
Classically, you can easily clone a bit. Consider a 2-bit system, $x, y$. Each bit can be 0 or 1. All 4 combos are possible.
Represent the state with a 4-vector
$s=\begin{vmatrix} a_0\\a_1\\a_2\\a_3\end{vmatrix}$
where exactly one $a_i=1$ and the other three are 0. E.g., if $a_3=1$ then $x=y=1$.
Here's a 2-input, 2-output circuit that clones the first bit.
$x'=x\\y'=x$
Its truth table is
x y | x'y'
0 0 | 0 0
0 1 | 0 0
1 0 | 1 1
1 1 | 1 1
Represent the operation by a matrix multiplication on s.
The matrix M is:
1 1 0 0
0 0 0 0
0 0 0 0
0 0 1 1
That is, the final state is $s'_i = \sum_j M_{ij} s_j$
However, M is singular. For quantum operations, M has to be unitary.
So this is not a legal quantum circuit. Let's try again.
The better way is the 3-input Toffoli gate. The function is
$x'=x \\ y'=y \\ z'= z \oplus xy$
The truth table is
x y z | x'y'z'
0 0 0 | 0 0 0
0 0 1 | 0 0 1
0 1 0 | 0 1 0
0 1 1 | 0 1 1
1 0 0 | 1 0 0
1 0 1 | 1 0 1
1 1 0 | 1 1 1
1 1 1 | 1 1 0
The matrix is Eqn 5.62 on page 155.:
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 0
Let x=1, z=0. Then:
x'= 1
y'= y
z'= y
and we've cloned y in the classical case, where the inputs are each 0 or 1.
This matrix is nonsingular and so is also legal in a quantum circuit.
(Looking ahead a little), try $y= \frac{1}{\sqrt{2}} | 0> + \frac{1}{\sqrt{2}} | 1>$, which is an equal superposition of 0 and 1. Using x=1, z=0, the input will be
$\frac{ | 1, 0, 0> + | 1, 1, 0>}{\sqrt{2}}$
and the state is
$(0, 0, 0, 0, \frac{1}{\sqrt{2}} , 0, \frac{1}{\sqrt{2}} , 0)^T$
That's an equal superposition of 2 of the possible 8 classical input states.
Multiplying that by the matrix gives
$\frac{ | 1, 0, 0> + | 1, 1, 1>}{\sqrt{2}}$
Instead of cloning y into z, this entangled y and z.
An operation that is simple on classical input can be more complicated on quantum inputs.
This isn't new; we already know how to entangle two qbits.
Engangling isn't the same as cloning. The point of cloning is that we could operate on the two bits separately. If they're engangled, operating on one affects the other.