Brief Algorithm




Next: DetailedEfficient, Algorithm
Up: Calculating the Area of
Previous: Theoretical Basis of
A sketch of the algorithm, ignoring efficiency considerations, now
appears as follows.
- Initialize a data structure to contain a list of triples,
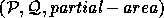 , to accumulate the
areas of the output polygons.
, to accumulate the
areas of the output polygons.  and
and  are the names of the
polygons from the first and second input maps respectively.
are the names of the
polygons from the first and second input maps respectively.
- Find all intersections of any edge of map 1 with any edge of map
2. Each intersection will generate 8 half-edges, as shown in figure
3.
=6.5in

Figure 3: The 8 Half-Edges Derived from One Intersection
- For each half-edge resulting from an intersection, find the
tangent and normal vectors and the relevant polygons from each input
map. Note that in figure 3 there are two polygons
from map 1, one on each side of edge 1, and also two from map 2, one on
each side of edge 2. Each of the 4 possible pairs of the input polygons
will apply to 2 of the 8 half-edges. For example, half-edges 1 and 5 are
part of the output polygon that is the intersection of the polygon on
map 1 above edge 1 with the polygon on map 2 to the right of edge
2.
- Apply the formula to each half-edge to calculate its contribution
to the relevant output polygon's area.
- Now we must calculate and process the half-edges not resulting
from an intersection. For each endpoint of each edge of map 1, determine
which polygon of map 2 contains it. Repeat for the edges of map
2.
- Split each edge of each input map into four half-edges.
- Apply the formula to these half-edges and store their partial
areas.
- Extract the final area of each non-empty output polygon, which was
the goal.
Wm Randolph Franklin
Wed Dec 14 14:03:28 EST 1994
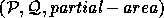 , to accumulate the
areas of the output polygons.
, to accumulate the
areas of the output polygons.  and
and  are the names of the
polygons from the first and second input maps respectively.
are the names of the
polygons from the first and second input maps respectively.

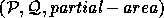 , to accumulate the
areas of the output polygons.
, to accumulate the
areas of the output polygons.  and
and  are the names of the
polygons from the first and second input maps respectively.
are the names of the
polygons from the first and second input maps respectively.
