Theoretical Basis of the Algorithm

The algorithm is built on the following principle. Many properties of a polygon, such as area, center of mass, and moments of inertia, may be calculated separately for each half-edge of the polygon and then summed. These are extensive properties in a thermodynamic sense, in that the total value for an object may be found by integrating over its area or volume. This concept is also related to Greene's theorem in calculus, where an integral over an area is transformed into an equivalent integral over the boundary of the area. Formally, let polygon P have the set of half-edges E. Let F(P) be some desired function of the polygon, such as area. Then for these F, there exists a functional that returns a new function such that

For example,

and

The basis of these formulæ is described in more detail in Franklin[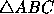 ]. However, the idea can be seen from figure 2, where is a polygon whose area we wish to determine. We partition it into six triangles by dropping perpendiculars from the origin, , to each side. Each smaller triangle, such as 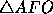, is determined by the local topology of the external edge 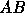at the vertex 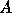. That is, 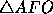is completely determined by the location of 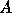(relative to ) and the direction of relative to 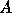. The total area of 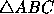can be found by summing the areas of the six smaller triangles. However, the area of each smaller triangle is one term of the formula 1.

  
Figure 2: Idea Behind the Local Topological Formulæ

So if we can find the half-edges of the output polygons we can find the areas. The output half-edges needed by the formulæ are of two types,

• those derived from an endpoint of an original edge of one of the input maps, or
• those derived from an intersection of two input map edges.

For each original endpoint we also need to know which polygon of the other map this point is in. For each intersection of two edges we already know the names of the relevant polygons.