Creating the one dimensional slab structure




Next: Degenerate cases
Up: DetailedEfficient, Algorithm
Previous: Locating the polygon
This section describes our point location algorithm in more detail.
- Each slab is one column of cells from the same grid used
later for edge intersection. The edges in the cells in a column
are gathered together and sorted primarily by their minimum Y
coordinates, and secondarily by their ID number. This comparison
predicate assures that two edges will not compare the same unless
they are the same edge. This results in duplicates of the same
edge being adjacent after the sort, so they can be
deleted. Duplicates occur when the same edge falls in more than
one cell in the column.
- Finally a selection sort is performed on the unduplicated
edges in each slab. The criterion is the partial order where one
edge is less than another if, from a viewpoint located at
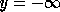 , the former edge (at least partly) obscures the latter
one. (A partial order is a relation that is not defined for all
pairs of objects. E.g., if we have a group of objects, some of
whom hide others, then ``hiding'' is a partial order. This
partial order was used early in Prism-map by
Franklin[ ].) After this step, the edges in each
slab are ordered so that if one edge at least partially hides
another, then the latter edge is later in the list.
, the former edge (at least partly) obscures the latter
one. (A partial order is a relation that is not defined for all
pairs of objects. E.g., if we have a group of objects, some of
whom hide others, then ``hiding'' is a partial order. This
partial order was used early in Prism-map by
Franklin[ ].) After this step, the edges in each
slab are ordered so that if one edge at least partially hides
another, then the latter edge is later in the list.
- To determine the polygon containing a point, first the slab
containing the point is determined. Then, the location of the
point in the partially ordered edges is determined, and a ray is
fired up from the point to the first edge that it hits, in the
order that the edges are stored in the slab. Then the point is in
this edge's left or right neighboring polygon depending on whether
the edge's first endpoint is to the right or left of its second
endpoint, respectively.




Next: Degenerate cases
Up: DetailedEfficient, Algorithm
Previous: Locating the polygon
Wm Randolph Franklin
Wed Dec 14 14:03:28 EST 1994
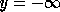 , the former edge (at least partly) obscures the latter
one. (A partial order is a relation that is not defined for all
pairs of objects. E.g., if we have a group of objects, some of
whom hide others, then ``hiding'' is a partial order. This
partial order was used early in Prism-map by
Franklin[ ].) After this step, the edges in each
slab are ordered so that if one edge at least partially hides
another, then the latter edge is later in the list.
, the former edge (at least partly) obscures the latter
one. (A partial order is a relation that is not defined for all
pairs of objects. E.g., if we have a group of objects, some of
whom hide others, then ``hiding'' is a partial order. This
partial order was used early in Prism-map by
Franklin[ ].) After this step, the edges in each
slab are ordered so that if one edge at least partially hides
another, then the latter edge is later in the list.