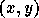 against a line
against a line 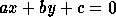 ,
and that we are using simulation of simplicity to pretend to shift
the point by
,
and that we are using simulation of simplicity to pretend to shift
the point by 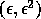 . Thus testing the point
. Thus testing the point
 against
against 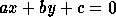 goes as
follows. Note that so long as
goes as
follows. Note that so long as 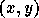 is not on the line, then
the same answer is returned as before.
is not on the line, then
the same answer is returned as before.
These occur when a vertex of one map falls on an edge or vertex of
the other. Although this has previously been a very difficult
problem, there is now a complete theoretical, and practical,
solution to the problem of degeneracies, the Simulation of
Simplicity technique of Edelsbrunner and Mücke
[ ]. Briefly, this pretends to add an
infinitesimal to the coordinates of the second map. By definition,
all first order infinitesimals are less than all positive finite
numbers. Different orders of infinitesimals may be used; all
second order ones are less than all first order ones, etc. A
delightful book on this is by Knuth [ ]. The
effect of infinitesimals is to prevent any comparison tests from
returning an equality. We do not actually store infinitesimals,
but instead determine what their effect would be on any test, and
code a modified test accordingly. The modified test is longer but
generally not significantly slower. For example, suppose that we
are testing a point 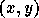 against a line
against a line 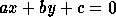 ,
and that we are using simulation of simplicity to pretend to shift
the point by
,
and that we are using simulation of simplicity to pretend to shift
the point by 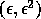 . Thus testing the point
. Thus testing the point
 against
against 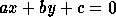 goes as
follows. Note that so long as
goes as
follows. Note that so long as 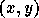 is not on the line, then
the same answer is returned as before.
is not on the line, then
the same answer is returned as before.
d=ax+by+c;
if (d0) then return signum(d);
else if (a0) then return signum(a);
else return signum(b);
signum returns -1, 0, or 1 according to the sign of its argument. Note that the extra tests are called only in the degenerate case. Now, one might deduce this particular test without resort to simulation of simplicity. However this technique provides a general, theoretically well-founded, method for creating all such tests.