Locating the polygon containing each edge endpoint




Next: Creating the one
Up: DetailedEfficient, Algorithm
Previous: Finding intersections
The naive method compares each point against each edge of the other map.
However, using a uniform grid again, this can be done in expected time
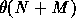 if there are N points to test against a map with
M edges. (The notation
if there are N points to test against a map with
M edges. (The notation 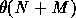 stands for any quantity that
grows proportionally to
stands for any quantity that
grows proportionally to  as they grow. Since it ignores constant
multiplicative factors, like
as they grow. Since it ignores constant
multiplicative factors, like  or
or 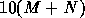 , it expresses
something that remains valid as the computer hardware changes. Of
course, this notation becomes useless if it hides a factor that is too
large.)
, it expresses
something that remains valid as the computer hardware changes. Of
course, this notation becomes useless if it hides a factor that is too
large.)
We use an optimized version of an implementation of a
one-dimensional grid, or slab, method by
V. Sivaswami[ ]. Sample execution times are part
of the example below. 55,068 points were each located in a map
with 2075 polygons defined by 76,215 vertices. The location time
on a 1993-vintage Sun 10/30 Sparcstation workstation was 2.33 CPU
seconds, or 42 microseconds per point. There was also
preprocessing time, but that is impossible to separate from the
rest of the overlay processing.
If the user is feeling pessimistic about the data, and worried
that the uniform grid might fail, then there do exist more
complicated but worst-case optimal methods, such as section 2.2.2,
Location of a Point in a Planar Subdivision, of
Preparata[, or Sarnak ]. A
typical time for these might be 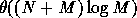 . However,
they are more difficult to implement. Some newer techniques work
by using a random sample of a subset of the data to build a
structure used for the point location. Sometimes the data
structure is designed to be dynamic, so that if some of the
polygons change, it does not need to be completely rebuilt. These
ideas are presented in Agarwal[ ],
Tamassia[, Stewart ],
Lee[, and Preparata ]. However,
many of these algorithms may have yet to be implemented.
. However,
they are more difficult to implement. Some newer techniques work
by using a random sample of a subset of the data to build a
structure used for the point location. Sometimes the data
structure is designed to be dynamic, so that if some of the
polygons change, it does not need to be completely rebuilt. These
ideas are presented in Agarwal[ ],
Tamassia[, Stewart ],
Lee[, and Preparata ]. However,
many of these algorithms may have yet to be implemented.




Next: Creating the one
Up: DetailedEfficient, Algorithm
Previous: Finding intersections
Wm Randolph Franklin
Wed Dec 14 14:03:28 EST 1994
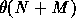 if there are N points to test against a map with
M edges. (The notation
if there are N points to test against a map with
M edges. (The notation 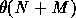 stands for any quantity that
grows proportionally to
stands for any quantity that
grows proportionally to  as they grow. Since it ignores constant
multiplicative factors, like
as they grow. Since it ignores constant
multiplicative factors, like  or
or 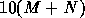 , it expresses
something that remains valid as the computer hardware changes. Of
course, this notation becomes useless if it hides a factor that is too
large.)
, it expresses
something that remains valid as the computer hardware changes. Of
course, this notation becomes useless if it hides a factor that is too
large.)
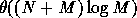 . However,
they are more difficult to implement. Some newer techniques work
by using a random sample of a subset of the data to build a
structure used for the point location. Sometimes the data
structure is designed to be dynamic, so that if some of the
polygons change, it does not need to be completely rebuilt. These
ideas are presented in Agarwal
. However,
they are more difficult to implement. Some newer techniques work
by using a random sample of a subset of the data to build a
structure used for the point location. Sometimes the data
structure is designed to be dynamic, so that if some of the
polygons change, it does not need to be completely rebuilt. These
ideas are presented in Agarwal