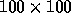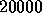We use Franklin's uniform grid method [
For typical grid resolutions, the number of grid cells is
proportional to the input+output size, so traversing the cell
matrix does not affect the asymptotic time. The grid resolution,
typically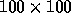 
has no relation to the resolution of the
coordinate representation, here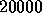 
.
The common objection is that the uniform grid is too simple for irregular data, since an adversary can easily produce bad input by placing many edges in one cell, to cause the pair-by-pair comparison of all the edges in each cell to take too much time. The answer is that in practice, it works, quite well, unless there are orders of magnitude variations. The robustness with respect to different choices of grid size is exemplified by using it to find all edge intersections in the United States Geological Survey Digital Line Graph sampler tape, for Chicamauga, Tennessee, which has both urban and rural road densities.
In that database, there are 116,896 edges, of an average length of 0.0023 of the map size. The edges' lengths are very skewed, with the standard deviation at 0.0081, or four times the average. There are 144,666 intersections in all, 135,875 of them where the endpoints of edges touch. We tested a large range of different grid resolutions, and observed a factor of three variation from the optimum grid size to cause only a 20% to 50% increase in time. This is a factor of 100 in the number of grid cells between the low and high grid resolutions, wherein the time remains reasonable. I.e, choosing the exact, optimum, grid size is not critical. This also explains why uneven data can be handled. A grid chosen for the average edge length and density will be different than the optimum grid for the data in specific regions of the scene; however so long as it is within a factor of three of the optimum grid resolution in that region, there is no problem. Figure 5 shows how the CPU time varies with the grid size when finding all the edge intersections in this database. As the grid gets finer, it takes more time to insert the edges into the cells. However, since each cell has fewer edges, processing the cells is quicker, until there are so many cells that the fixed per-cell overhead starts to dominate.
=7in
Figure 5: Intersection Time vs Grid Size