Engineering Probability Class 6 Mon 2018-02-05

Event A is that a random person has a lycanthopy gene. Assume P(A) = .01.

Genes-R-Us has a DNA test for this. B is the event of a positive test. There are false positives and false negatives each w.p. (with probability) 0.1. That is, P(B|A') = P(B' | A) = 0.1

What's P(A')?

1. 0.09
2. .099
3. .189
4. .48
5. .99

What's P(A and B)?

1. 0.09
2. .099
3. .189
4. .48
5. .99

What's P(A' and B)?

1. 0.09
2. .099
3. .189
4. .48
5. .99

What's P(B)?

1. 0.09
2. .099
3. .189
4. .48
5. .99

You test positive. What's the probability you're really positive, P(A|B)?

1. 0.09
2. .099
3. .189
4. .48
5. .99

Wikipedia on Bayes theorem.

We'll do the second example in class.

Look at example 2.30 chip quality control: For example 2.28, how long do we have to burn in chips so that the survivors have a 99% probability of being good? p=0.1, a=1/20000. I may do it on Thurs.

2.5 Independent events

1. \(P[A\cap B] = P[A] P[B]\)
2. P[A|B] = P[A], P[B|A] = P[B]

A,B independent means that knowing A doesn't help you with B.

Mutually exclusive events w.p.>0 must be dependent.

Example 2.33. Last condition above is required.

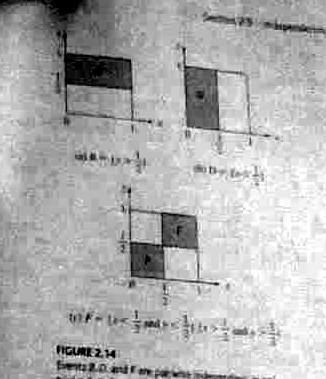
More that 2 events:

1. N events are independent iff the occurrence of no combo of the events affects another event.
2. Each pair is independent.
3. Also need \(P[A\cap B\cap C] = P[A] P[B] P[C]\)
4. This is not intuitive A, B, and C might be pairwise independent, but, as a group of 3, are dependent.
5. See example 2.32, page 55. A: x>1/2. B: y>1/2. C: x>y

Common application: independence of experiments in a sequence.

Example 2.34: coin tosses are assumed to be independent of each other.

P[HHT] = P[1st coin is H] P[2nd is H] P[3rd is T].

Example 2.35 System reliability

1. Controller and 3 peripherals.
2. System is up iff controller and at least 2 peripherals are up.
3. Add a 2nd controller.

2.6 p59 Sequential experiments: maybe independent

2.6.1 Sequences of independent experiments

1. Example 2.36

2.6.2 Binomial probability

1. Bernoulli trial flip a possibly unfair coin once. p is probability of head.
2. (Bernoulli did stats, econ, physics, ... in 18th century.)

Example 2.37

1. P[TTH] = \((1-p)^2 p\)
2. P[1 head] = \(3 (1-p)^2 p\)

Probability of exactly k successes = \(p_n(k) = {n \choose k} p^k (1-p)^{n-k}\)

\(\sum_{k=0}^n p_n(k) = 1\)

Example 2.38

Can avoid computing n! by computing \(p_n(k)\) recursively, or by using approximation. Also, in C++, using double instead of float helps. (Almost always you should use double instead of float. It's the same speed.)

Example 2.39

Example 2.40 Error correction coding

Multinomial probability law

1. There are M different possible outcomes from an experiment, e.g., faces of a die showing.

2. Probability of particular outcome: \(p_i\)

3. Now run the experiment n times.

4. Probability that i-th outcome occurred \(k_i\) times, \(\sum_{i=1}^M k_i = n\)

   \begin{equation*} P[(k_1,k_2,...,k_M)]` :math:`= \frac{n!}{k_1! k_2! ... k_M!} p_1^{k_1} p_2^{k_2}...p_M^{k_M} \end{equation*}

Example 2.41 dartboard.

Example 2.42 random phone numbers.

2.7 Computer generation of random numbers

1. Skip this section, except for following points.
2. Executive summary: it's surprisingly hard to generate good random numbers. Commercial SW has been known to get this wrong. By now, they've gotten it right (I hope), so just call a subroutine.
3. Arizona lottery got it wrong in 1998.
4. Even random electronic noise is hard to use properly. The best selling 1955 book A Million Random Digits with 100,000 Normal Deviates had trouble generating random numbers this way. Asymmetries crept into their circuits perhaps because of component drift. For a laugh, read the reviews.
5. Pseudo-random number generator: The subroutine returns numbers according to some algorithm (e.g., it doesn't use cosmic rays), but for your purposes, they're random.
6. Computer random number routines usually return the same sequence of number each time you run your program, so you can reproduce your results.
7. You can override this by seeding the generator with a genuine random number from linux /dev/random.

2.8 and 2.9 p70 Fine points: Skip.

Review Bayes theorem, since it is important. Here is a fictitious (because none of these probilities have any justification) SETI example.

1. A priori probability of extraterrestrial life = P[L] = \(10^{-8}\).
2. For ease of typing, let L' be the complement of L.
3. Run a SETI experiment. R (for Radio) is the event that it has a positive result.
4. P[R|L] = \(10^{-5}\), P[R|L'] = \(10^{-10}\).
5. What is P[L|R] ?

Some specific probability laws

1. In all of these, successive events are independent of each other.
2. A Bernoulli trial is one toss of a coin where p is probability of head.
3. We saw binomial and multinomial probilities on Tues.
4. The binomial law gives the probability of exactly k heads in n tosses of an unfair coin.
5. The multinomial law gives the probability of exactly ki occurrances of the i-th face in n tosses of a die.

iClicker: You have a coin where the probability of a head is p=2/3 If you toss it twice, what's the probability that you will see one head and one tail?

1. 1/2
2. 1/3
3. 2/9
4. 5/9
5. 4/9

2.6.4 p63 Geometric probability law

1. Repeat Bernoulli experiment until 1st success.
2. Define outcome to be # trials until that happens.
3. Define q=(1-p).
4. \(p(m) = (1-p)^{m-1}p = q^{m-1}p\) (p has 2 different uses here).
5. \(\sum_{m=1}^\infty p(m) =1\)
6. Probability that more than K trials are required = \(q^K\).

Example: probability that more than 10 tosses of a die are required to get a 6 = \(\left(\frac{5}{6}\right)^{10} = 0.16\)

iClicker: You have a coin where the probability of a head is p=2/3 What's the probability that the 1st head occurs on the 2nd toss?

1. 1/2
2. 1/3
3. 2/9
4. 5/9
5. 4/9

Example 2.43: error control by retransmission. A sent over a noisy channel is checksummed so the receiver can tell if it got mangled, and then ask for retransmission. TCP/IP does this.

Aside: This works better when the roundtrip time is reasonable. Using this when talking to Mars is challenging.

2.6.5 p64 Sequences, chains, of dependent experiments.

1. This is an important topic, but mostly beyond this course.
2. In many areas, there are a sequence of observations, and the probability of each observation depends on what you observed before.
3. It relates to Markov chains.
4. Motivation: speech and language recognition, translation, compression
5. E.g., in English text, the probability of a u is higher if the previous char was q.
6. The probability of a b may be higher if the previous char was u (than if it was x), but is lower if the previous two chars are qu.
7. Need to look at probabilities of sequences, char by char.
8. Same idea in speech recognition: phonemes follow phonemes...
9. Same in language understanding: verb follows noun...

Example 2.44, p64

1. In this example, you repeatedly choose an urn to draw a ball from, depending on what the previous ball was.