Bresenham Line and Circle Drawing

Bresenham Algorithm - Optimized Line Drawing Code

We want to draw a line from (0,0) to (x1,y1), where 0<=y1<=x1, by setting one pixel per column. For example, if x=10, y=7, we get this:

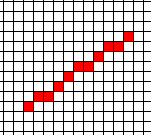
Here are several versions, ending with Bresenham's algorithm. The point of this is to use the simplest possible operations.

Simple program:

     m=y1/x1;
     pixel(0,0);
     for(x=1;x<=x1;x++) 
     { y=round(m*x);
       pixel(x,y);
     }

Track the deviation of the current y from the perfect line. When the deviation gets too large, increment y, and decrement the deviation.

    m=y1/x1;
    d=0;
    pixel(0,0);
    y=0;
    for(x=1;x<=x1;x++)
    {  d+= m;
       if (d>= 1/2) 
       {  d -= 1;
          y++;  }
       pixel(x,y);
    }

Scale up m and d by 2x to convert fractions to integers. This is ok since they are used only in the if; and it still branches at the same times as before.

    m=2*y1;
    d=0;
    pixel(0,0);
    y=0;
    for(x=1;x<=x1;x++)
    {  d+= m;
       if (d>=x1)
       {  d-= 2*x1;
          y++;}
       pixel(x,y);
    }

Shift d by -x1 to remove a subtraction.

    m=2*y1;
    d= -x1;
    pixel(0,0);
    y=0;
    for(x=1;x<=x1;x++)
    {  d+= m;
       if (d>=0)
       {  d-= 2*x1;
          y++;}
       pixel(x,y);
    }

Assume that the pixels are stored in a framebuffer, and that pixel_{x y} is stored at location fb+x*maxy+y where fb is the address of the start of the framebuffer, and maxy is the max value of y in the framebuffer, i.e., 0<= y<= y1<= maxy. Then we get:
```
    m=2*y1;
    d= -x1;
    *fb=1;
    y=0;
    for(x=1;x<=x1;x++)
    {  d+= m;
       if (d>=0)
       {  d-= 2*x1;
          y++;}
       *(fb+x*maxy+y)=1;
    }
```

Letting p be the current address, we can optimize.

    m=2*y1;
    d= -x1;
    p=fb;
    *p=1;
    for(x=1;x<=x1;x++)
    {  d+= m;
       p+=maxy;
       if (d>=0)
       {  d-= 2*x1;
          p++;}
       *p=1;
    }

The next problem is that modern computers use a pipelined architecture, where different stages of several instructions are processed in parallel. However, when there is a conditional, the computer can't tell what the next instructions are, and so is forced to flush the pipeline. Therefore we want to eliminate the conditional in the inner loop. The following assumes that the right shift is arithmetic.
Mask is all ones when d>=0, all zeroes otherwise.
We also pulled 2*x1 out of the loop.
```
    m=2*y1;
    d= -x1;
    p=fb;
    *p=1;
    doublex1= x1<1;
    for(x=1;x<=x1;x++)
    {  d+= m;
       p+=maxy;
       mask = (~(d>>31));  
       d -=  (doublex1&mask);
       p += (1&mask);
       *p=1;
    }
```
We can also offset x by x1 so that the termination condition is a test against 0.

Bresenham Circle Algorithm

Here are several ways to draw a circle, ending with the Bresenham circle algorithm.

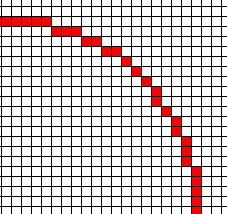
Taylor series for sqrt(1-x²), in the 2nd octant: 0<= x<= y, where the curve doesn't get too vertical. The following is expanded about the origin. The error at x=.71 is 0.0003.
y(x) = 1 - (1/2) x² - (1/8) x⁴ - (1/16) x⁶ - (5/128) x⁸ - (7/256) x¹⁰ - (21/1024) x ¹²+ ...
This is popular but usually the wrong way.
If you must use Taylor, at least expand about the center of the interval:
z = x- 0.3536
y(z) = ( 0.9353967287- 0.3780214203 z- 0.6109173568
z² - 0.2468897312 z³ - 0.2992736736
z⁴ - 0.2821915805 z⁵ - 0.3420828869
z⁶ - 0.4015387039 z⁷ - 0.5080487872
z⁸ - 0.6481416197 z⁹ - 0.8517407025
z¹⁰ - 1.133286086 z¹¹ - 1.531581071
z¹² - 2.091410948 z¹³+...
The error at x=.71 is 0.000 004. This is better, but there are more nonzero coefficients, which means that it is slower.
A Chebyshev series, which tries to minimize the maximum error over an interval beats a Taylor series:
y(x) = + 1.000000093 - 0.00002511816061 x - 0.4988901592
x² - 0.01882886918 x³ + 0.03498610076
x⁴ - 0.7655182976 x⁵ + 2.101697099
x⁶ - 3.603814683 x⁷ + 3.259950635
x⁸ - 1.315059748 x⁹
This has a max error of 1.5*10^-7, which is much better than above, expecially as there are only 8 coefficients. We could get as good as either Taylor with many fewer terms than they.
Rotate the point (R,0) by DΘ repeatedly (Θ is the angle). What should DΘ be?
Approximate the rotation matrix:

cos Θ sin Θ

- sin Θ cos Θ

approximately =
1 Θ

-Θ 1

with everything multiplied by R. But this circle may grow since the determinant >1.
Improve the approx matrix so the determinant =1:
1 Θ

-Θ 1-Θ²
Binomial theorem on sqrt(1-x²). Does this do the same as Taylor expanded about 0?
Here are two parametric ways to draw circles.
1. x = R cos Θ
  y = R sin Θ
  What should DΘ be?
2. x = R (2t)/(t²+1}
  y = R (t²-1)/(t²+1) ; -infinity<t<infinity
  Unfortunately, the speed of the curve wrt t varies with t, so the stepsize must also.
  Note that t is not an angle, but just the name for the parameter.
There is no parametric polynomial, of any degree, that exactly represents a circle. However you can get good approximations.
Assume that memory is cheap and that the user may draw circles with the same size several times. Therefore: when you compute a circle, save its pixels for future use.
Can we compute a small circle as a scaling down of a large circle?
Start from the system of differential equations:

    dx/dt = -y
    dy/dt = x

with x(0) = R. The trick is to prevent the circle from spiraling in or out. A trapezoid rule may be useful.

???? (You suggest)

Now let's optimize C code. Do the second octant only.

    pixel(0,r);
    for(x=1;x<r/sqrt(2);x++)
    {  y=sqrt(r^2-x^2);
       pixel(x,y);
    }

Assume that the last point was (x-1,y). Find whether (x,y-½) is above or below the circle, and move SE to (x,y-1) or E to (x,y), respectively.
```
    y=r;
    pixel(0,r);
    for(x=1;x<r/sqrt(2);x++)
    {  d=x^2+(y-1/2)^2-r^2;
       if (d>=0) y--;
       pixel(x,y);
    }
```
Optimize:
d=x²+(y-1/2)²-r² becomes d=x²+y²-y+1/4-r² . How does the d for a given x differ from d for x-1? If y is unchanged, then d_x = d_x-1+2x-1. If y decreases, add -2y+2, where that is the old y. Also the only time that 1/4 affects the test d>0 is when d=1/4, so ignore it, but make the test d>=0.
```
    y=r;
    d= -r;
    pixel(0,r);
    for(x=1;x<r/sqrt(2);x++)
    {  d+= 2x-1;
       if (d>=0) 
       {  y--;
          d -= 2y; /* Must do this AFTER y-- */
       }
       pixel(x,y);
    }
```
This is Bresenham's circle algorithm. Note that you can store 2x-1 and -2y and update them by adding or subtracting 2.

Lo-level optimizations can also be done thus:

    y=r;
    d= -r;
    x2m1= -1;
    pixel(0,r);
    for(x=1;x<r/sqrt(2);x++)
    {  x2m1 += 2;
       d+= x2m1;
       if (d>=0) 
       {  y--;
          d -= (y<<1);  /* Must do this AFTER y-- */
       }
       pixel(x,y);
    }

You can also do the same pipelining techniques used for the line algorithm.
Finally, on an Intel processor, there are ways to use the available instructions efficiently.

cos Θ	sin Θ
- sin Θ	cos Θ

1	Θ
-Θ	1

1	Θ
-Θ	1-Θ²