Skip to main content

Engineering Probability Class 4 Mon 2020-01-27

Source

2   Chapter 2 ctd

  1. Today: counting methods, Leon-Garcia section 2.3, page 41.

    1. We have an urn with n balls.
    2. Maybe the balls are all different, maybe not.
    3. W/o looking, we take k balls out and look at them.
    4. Maybe we put each ball back after looking at it, maybe not.
    5. Suppose we took out one white and one green ball. Maybe we care about their order, so that's a different case from green then white, maybe not.

  2. Applications:

    1. How many ways can we divide a class of 12 students into 2 groups of 6?
    2. How many ways can we pick 4 teams of 6 students from a class of 88 students (leaving 64 students behind)?
    3. We pick 5 cards from a deck. What's the probability that they're all the same suit?
    4. We're picking teams of 12 students, but now the order matters since they're playing baseball and that's the batting order.
    5. We have 100 widgets; 10 are bad. We pick 5 widgets. What's the probability that none are bad? Exactly 1? More than 3?
    6. In the approval voting scheme, you mark as many candidates as you please. The candidate with the most votes wins. How many different ways can you mark the ballot?
    7. In preferential voting, you mark as many candidates as you please, but rank them 1,2,3,... How many different ways can you mark the ballot?

  3. Leon-Garcia 2.3: Counting methods, pp 41-46.

    1. finite sample space
    2. each outcome equally probable
    3. get some useful formulae
    4. warmup: consider a multiple choice exam where 1st answer has 3 choices, 2nd answer has 5 choices and 3rd answer has 6 choices.
      1. Q: How many ways can a student answer the exam?
      2. A: 3x5x6
    5. If there are k questions, and the i-th question has \(n_i\) answers then the number of possible combinations of answers is \(n_1n_2 .. n_k\)

  4. 2.3.1 Sampling WITH replacement and WITH ordering

    1. Consider an urn with n different colored balls.
    2. Repeat k times:
      1. Draw a ball.
      2. Write down its color.
      3. Put it back.
    3. Number of distinct ordered k-tuples = \(n^k\)

  5. Example 2.1.5. How many distinct ordered pairs for 2 balls from 5? 5*5.

  6. Review. Suppose I want to eat one of the following 4 places, for tonight and again tomorrow, and don't care if I eat at the same place both times: Commons, Sage, Union, Knotty Pine. How many choices to I have where to eat?

    1. 16
    2. 12
    3. 8
    4. 4
    5. something else

  7. 2.3.2 Sampling WITHOUT replacement and WITH ordering

    1. Consider an urn with n different colored balls.
    2. Repeat k times:
      1. Draw a ball.
      2. Write down its color.
      3. Don't put it back.
    3. Number of distinct ordered k-tuples = n(n-1)(n-2)...(n-k+1)

  8. Review. Suppose I want to visit two of the following four cities: Buffalo, Miami, Boston, New York. I don't want to visit one city twice, and the order matters. How many choices to I have how to visit?

    1. 16
    2. 12
    3. 8
    4. 4
    5. something else

  9. Example 2.1.6: Draw 2 balls from 5 w/o replacement.

    1. 5 choices for 1st ball, 4 for 2nd. 20 outcomes.
    2. Probability that 1st ball is larger?
    3. List the 20 outcomes. 10 have 1st ball larger. P=1/2.

  10. Example 2.1.7: Draw 3 balls from 5 with replacement. What's the probability they're all different?

    1. P = \(\small \frac{\text{# cases where they're different}}{\text{# cases where I don't care}}\)
    2. P = \(\small \frac{\text{# case w/o replacement}}{\text{# cases w replacement}}\)
    3. P = \(\frac{5*4*3}{5*5*5}\)

  11. 2.3.3 Permutations of n distinct objects

    1. Distinct means that you can tell the objects apart.

    2. This is sampling w/o replacement for k=n

    3. 1.2.3.4...n = n!

    4. It grows fast. 1!=1, 2!=2, 3!=6, 4!=24, 5!=120, 6!=720, 7!=5040

    5. Stirling approx:

      \begin{equation*} n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^n\left(1+\frac{1}{12n}+...\right) \end{equation*}

    6. Therefore if you ignore the last term, the relative error is about 1/(12n).

  12. Example 2.1.8. # permutations of 3 objects. 6!

  13. Example 2.1.9. 12 airplane crashes last year. Assume independent, uniform, etc, etc. What's probability of exactly one in each month?

    1. For each crash, let the outcome be its month.
    2. Number of events for all 12 crashes = \(12^{12}\)
    3. Number of events for 12 crashes in 12 different months = 12!
    4. Probability = \(12!/(12^{12}) = 0.000054\)
    5. Random does not mean evenly spaced.

  14. 2.3.4 Sampling w/o replacement and w/o ordering

    1. We care what objects we pick but not the order

    2. E.g., drawing a hand of cards.

    3. term: Combinations of k objects selected from n. Binomial coefficient.

      \begin{equation*} C^n_k = {n \choose k} = \frac{n!}{k! (n-k)!} \end{equation*}

    4. Permutations is when order matters.

  15. Example 2.20. Select 2 from 5 w/o order. \(5\choose 2\)

  16. Example 2.21 # permutations of k black and n-k white balls. This is choosing k from n.

  17. Example 2.22. 10 of 50 items are bad. What's probability 5 of 10 selected randomly are bad?

    1. # ways to have 10 bad items in 50 is \(50\choose 10\)
    2. # ways to have exactly 5 bad is 3 ways to select 5 good from 40 times # ways to select 5 bad from 10 = \({40\choose5} {10\choose5}\)
    3. Probability is ratio.

  18. Multinomial coefficient: Partition n items into sets of size \(k_1, k_2, ... k_j, \sum k_i=n\)

    \begin{equation*} \frac{n!}{k_1! k_2! ... k_j!} \end{equation*}

  19. 2.3.5. skip

Reading: 2.4 Conditional probability, page 47-

3   Review questions

  1. Retransmitting a very noisy bit 2 times: The probability of each bit going bad is 0.4. What is probability of no error at all in the 2 transmissions?
    1. 0.16
    2. 0.4
    3. 0.36
    4. 0.48
    5. 0.8
  2. Flipping an unfair coin 2 times: The probability of each toss being heads is 0.4. What is probability of both tosses being tails?
    1. 0.16
    2. 0.4
    3. 0.36
    4. 0.48
    5. 0.8
  3. Flipping a fair coin until we get heads: How many times will it take until the probability of seeing a head is >=.8?
    1. 1
    2. 2
    3. 3
    4. 4
    5. 5
  4. This time, the coin is weighted so that p[H]=.6. How many times will it take until the probability of seeing a head is >=.8?
    1. 1
    2. 2
    3. 3
    4. 4
    5. 5

4   Review

  1. Followon to the meal choice review question. My friend and I wish to visit a hospital, chosen from: Memorial, AMC, Samaritan. We might visit different hospitals.
    1. If we don't care whether we visit the same hospital or not, in how many ways can we do this?
      1. 1
      2. 2
      3. 3
      4. 6
      5. 9
    2. We wish to visit different hospitals, to later write a Poly review. In how many ways can we visit different hospitals, where we care which hospital each of us visits?
      1. 1
      2. 2
      3. 3
      4. 6
      5. 9
    3. Modify the above, to say that we care only about the set of hospitals we two visit.
      1. 1
      2. 2
      3. 3
      4. 6
      5. 9
    4. We realize that Samaritan and Memorial are both owned by St Peters and we want to visit two different hospital chains to write our reviews. In how many ways can we pick hospitals so that we pick different chains?
      1. 1
      2. 2
      3. 3
      4. 4
      5. 5
    5. We each pick between Memorial and AMC with 50% probability, independently. What is the probability that each hospital is picked exactly once (in contrast to picking one twice and the other not at all).
      1. 0
      2. 1/4
      3. 1/2
      4. 3/4
      5. 1

5   Chapter 2 ctd

  1. New stuff, pp. 47-66:

    1. Conditional probability - If you know that event A has occurred, does that change the probability that event B has occurred?
    2. Independence of events - If no, then A and B are independent.
    3. Sequential experiments - Find the probability of a sequence of experiments from the probabilities of the separate steps.
    4. Binomial probabilities - tossing a sequence of unfair coins.
    5. Multinomial probabilities - tossing a sequence of unfair dice.
    6. Geometric probabilities - toss a coin until you see the 1st head.
    7. Sequences of dependent experiments - What you see in step 1 influences what you do in step 2.

  2. 2.4 Conditional probability, page 47.

    1. big topic
    2. E.g., if it snows today, is it more likely to snow tomorrow? next week? in 6 months?
    3. E.g., what is the probability of the stock market rising tomorrow given that (it went up today, the deficit went down, an oil pipeline was blown up, ...)?
    4. What's the probability that a CF bulb is alive after 1000 hours given that I bought it at Walmart?
    5. definition \(P[A|B] = \frac{P[A\cap B]}{P[B]}\)

  3. E.g., if DARPA had been allowed to run its Futures Markets Applied to Prediction (FutureMAP) would the future probability of King Zog I being assassinated be dependent on the amount of money bet on that assassination occurring?

    1. Is that good or bad?
    2. Would knowing that the real Zog survived over 55 assassination attempts change the probability of a future assassination?

  4. Consider a fictional university that has both undergrads and grads. It also has both Engineers and others:

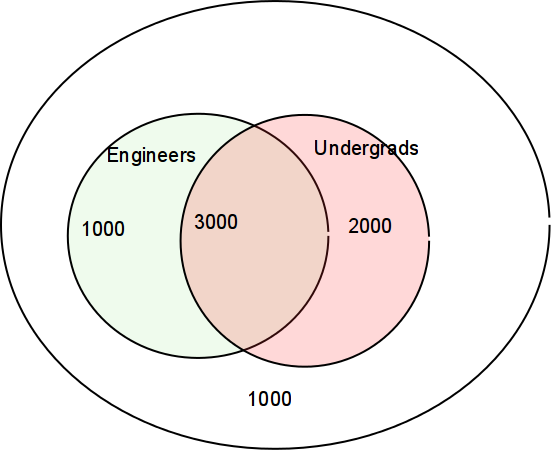
    /images/venn-stu.png

  5. Review: What's the probability that a student is an Engineer?

    1. 1/7
    2. 4/7
    3. 5/7
    4. 3/4
    5. 3/5

  6. Review: What's the probability that a student is an Engineer, given that s/he is an undergrad?

    1. 1/7
    2. 4/7
    3. 5/7
    4. 3/4
    5. 3/5

  7. \(P[A\cap B] = P[A|B]P[B] = P[B|A]P[A]\)

  8. Example 2.26 Binary communication. Source transmits 0 with probability (1-p) and 1 with probability p. Receiver errs with probability e. What are probabilities of 4 events?

  9. Total probability theorem

    1. \(B_i\) mutually exclusive events whose union is S
    2. P[A] = P[A \(\cap B_1\) + P[A \(\cap B_2\) + ...
    3. \(P[A] = P[A|B_1]P[B_1]\) \(+ P[A|B_2]P[B_2] + ...\)
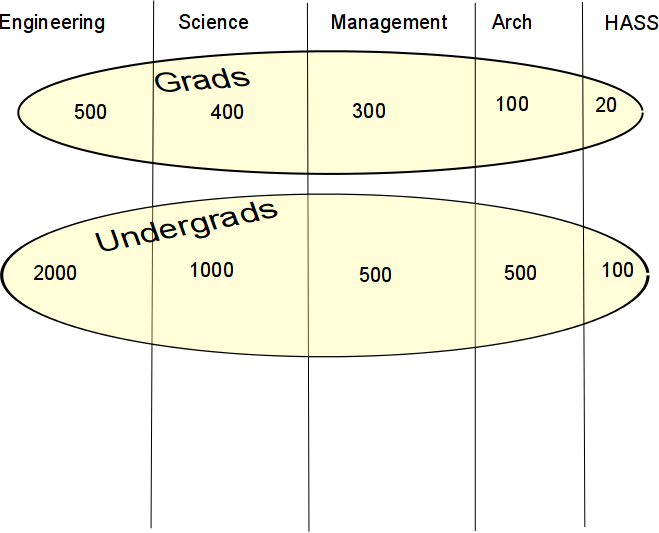
    /images/totalprob.png

    What's the probability that a student is an undergrad, given ... (Numbers are fictitious.)

  10. Example 2.28. Chip quality control.

    1. Each chip is either good or bad.
    2. P[good]=(1-p), P[bad]=p.
    3. If the chip is good: P[still alive at t] = \(e^{-at}\)
    4. If the chip is bad: P[still alive at t] = \(e^{-1000at}\)
    5. What's the probability that a random chip is still alive at t?

  11. 2.4.1, p52. Bayes' rule. This lets you invert the conditional probabilities.

    1. \(B_j\) partition S. That means that
      1. If \(i\ne j\) then \(B_i\cap B_j=\emptyset\) and
      2. \(\bigcup_i B_i = S\)
    2. \(P[B_j|A] = \frac{B_j\cap A}{P[A]}\) \(= \frac{P[A|B_j] P[B_j]}{\sum_k P[A|B_k] P[B_k]}\)
    3. application:
      1. We have a priori probs \(P[B_j]\)
      2. Event A occurs. Knowing that A has happened gives us info that changes the probs.
      3. Compute a posteriori probs \(P[B_j|A]\)

  12. In the above diagram, what's the probability that an undergrad is an engineer?

  13. Example 2.29 comm channel: If receiver sees 1, which input was more probable? (You hope the answer is 1.)

  14. Example 2.30 chip quality control: For example 2.28, how long do we have to burn in chips so that the survivors have a 99% probability of being good? p=0.1, a=1/20000.

  15. Example: False positives in a medical test

    1. T = test for disease was positive; T' = .. negative
    2. D = you have disease; D' = .. don't ..
    3. P[T|D] = .99, P[T' | D'] = .95, P[D] = 0.001
    4. P[D' | T] (false positive) = 0.98 !!!