Engineering Probability Class 6 Thurs 2019-01-31

Event A is that a random person has a lycanthopy gene. Assume P(A) = .01.

Genes-R-Us has a DNA test for this. B is the event of a positive test. There are false positives and false negatives each w.p. (with probability) 0.1. That is, P(B|A') = P(B' | A) = 0.1

What's P(A')?

1. 0.09
2. .099
3. .189
4. .48
5. .99

What's P(A and B)?

1. 0.09
2. .099
3. .189
4. .48
5. .99

What's P(A' and B)?

1. 0.09
2. .099
3. .189
4. .48
5. .99

What's P(B)?

1. 0.09
2. .099
3. .189
4. .48
5. .99

You test positive. What's the probability you're really positive, P(A|B)?

1. 0.09
2. .099
3. .189
4. .48
5. .99

2.5 Independent events

1. \(P[A\cap B] = P[A] P[B]\)
2. P[A|B] = P[A], P[B|A] = P[B]

A,B independent means that knowing A doesn't help you with B.

Mutually exclusive events w.p.>0 must be dependent.

Example 2.33, page 56.

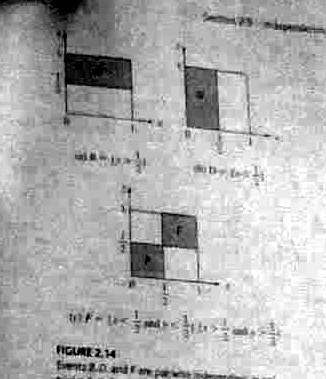
More that 2 events:

1. N events are independent iff the occurrence of no combo of the events affects another event.
2. Each pair is independent.
3. Also need \(P[A\cap B\cap C] = P[A] P[B] P[C]\)
4. This is not intuitive A, B, and C might be pairwise independent, but, as a group of 3, are dependent.
5. See example 2.32, page 55. A: x>1/2. B: y>1/2. C: x>y

Common application: independence of experiments in a sequence.

Example 2.34: coin tosses are assumed to be independent of each other.

P[HHT] = P[1st coin is H] P[2nd is H] P[3rd is T].

Example 2.35, page 58. System reliability

1. Controller and 3 peripherals.
2. System is up iff controller and at least 2 peripherals are up.
3. Add a 2nd controller.

2.6 p59 Sequential experiments: maybe independent

2.6.1 Sequences of independent experiments

1. Example 2.36

2.6.2 Binomial probability

1. Bernoulli trial flip a possibly unfair coin once. p is probability of head.
2. (Bernoulli did stats, econ, physics, ... in 18th century.)

Example 2.37

1. P[TTH] = \((1-p)^2 p\)
2. P[1 head] = \(3 (1-p)^2 p\)

Probability of exactly k successes = \(p_n(k) = {n \choose k} p^k (1-p)^{n-k}\)

\(\sum_{k=0}^n p_n(k) = 1\)

Example 2.38

Can avoid computing n! by computing \(p_n(k)\) recursively, or by using approximation. Also, in C++, using double instead of float helps. (Almost always you should use double instead of float. It's the same speed.)

Example 2.39

Example 2.40 Error correction coding

Multinomial probability law

1. There are M different possible outcomes from an experiment, e.g., faces of a die showing.

2. Probability of particular outcome: \(p_i\)

3. Now run the experiment n times.

4. Probability that i-th outcome occurred \(k_i\) times, \(\sum_{i=1}^M k_i = n\)

   \begin{equation*} P[(k_1,k_2,...,k_M)]` :math:`= \frac{n!}{k_1! k_2! ... k_M!} p_1^{k_1} p_2^{k_2}...p_M^{k_M} \end{equation*}

Example 2.41 dartboard.

Example 2.42 random phone numbers.

2.7 Computer generation of random numbers

1. Skip this section, except for following points.
2. Executive summary: it's surprisingly hard to generate good random numbers. Commercial SW has been known to get this wrong. By now, they've gotten it right (I hope), so just call a subroutine.
3. Arizona lottery got it wrong in 1998.
4. Even random electronic noise is hard to use properly. The best selling 1955 book A Million Random Digits with 100,000 Normal Deviates had trouble generating random numbers this way. Asymmetries crept into their circuits perhaps because of component drift. For a laugh, read the reviews.
5. Pseudo-random number generator: The subroutine returns numbers according to some algorithm (e.g., it doesn't use cosmic rays), but for your purposes, they're random.
6. Computer random number routines usually return the same sequence of number each time you run your program, so you can reproduce your results.
7. You can override this by seeding the generator with a genuine random number from linux /dev/random.

2.8 and 2.9 p70 Fine points: Skip.

Review Bayes theorem, since it is important. Here is a fictitious (because none of these probilities have any justification) SETI example.

1. A priori probability of extraterrestrial life = P[L] = \(10^{-8}\).
2. For ease of typing, let L' be the complement of L.
3. Run a SETI experiment. R (for Radio) is the event that it has a positive result.
4. P[R|L] = \(10^{-5}\), P[R|L'] = \(10^{-10}\).
5. What is P[L|R] ?

Some specific probability laws

1. In all of these, successive events are independent of each other.
2. A Bernoulli trial is one toss of a coin where p is probability of head.
3. We saw binomial and multinomial probilities in class 4.
4. The binomial law gives the probability of exactly k heads in n tosses of an unfair coin.
5. The multinomial law gives the probability of exactly ki occurrances of the i-th face in n tosses of a die.

iClicker: You have a coin where the probability of a head is p=2/3 If you toss it twice, what's the probability that you will see one head and one tail?

1. 1/2
2. 1/3
3. 2/9
4. 5/9
5. 4/9