Engineering Probability Class 5 Mon 2019-01-28

Source

1   Iclicker review

  1. Followon to the meal choice iclicker question. My friend and I wish to visit a hospital, chosen from: Memorial, AMC, Samaritan. We might visit different hospitals.
    1. If we don't care whether we visit the same hospital or not, in how many ways can we do this?
      1. 1
      2. 2
      3. 3
      4. 6
      5. 9
    2. We wish to visit different hospitals, to later write a Poly review. In how many ways can we visit different hospitals, where we care which hospital each of us visits?
      1. 1
      2. 2
      3. 3
      4. 6
      5. 9
    3. Modify the above, to say that we care only about the set of hospitals we two visit.
      1. 1
      2. 2
      3. 3
      4. 6
      5. 9
    4. We realize that Samaritan and Memorial are both owned by St Peters and we want to visit two different hospital chains to write our reviews. In how many ways can we pick hospitals so that we pick different chains?
      1. 1
      2. 2
      3. 3
      4. 4
      5. 5
    5. We each pick between Memorial and AMC with 50% probability, independently. What is the probability that each hospital is picked exactly once (in contrast to picking one twice and the other not at all).
      1. 0
      2. 1/4
      3. 1/2
      4. 3/4
      5. 1

2   Chapter 2 ctd

  1. New stuff, pp. 47-66:

    1. Conditional probability - If you know that event A has occurred, does that change the probability that event B has occurred?
    2. Independence of events - If no, then A and B are independent.
    3. Sequential experiments - Find the probability of a sequence of experiments from the probabilities of the separate steps.
    4. Binomial probabilities - tossing a sequence of unfair coins.
    5. Multinomial probabilities - tossing a sequence of unfair dice.
    6. Geometric probabilities - toss a coin until you see the 1st head.
    7. Sequences of dependent experiments - What you see in step 1 influences what you do in step 2.

  2. 2.4 Conditional probability, page 47.

    1. big topic
    2. E.g., if it snows today, is it more likely to snow tomorrow? next week? in 6 months?
    3. E.g., what is the probability of the stock market rising tomorrow given that (it went up today, the deficit went down, an oil pipeline was blown up, ...)?
    4. What's the probability that a CF bulb is alive after 1000 hours given that I bought it at Walmart?
    5. definition \(P[A|B] = \frac{P[A\cap B]}{P[B]}\)

  3. E.g., if DARPA had been allowed to run its Futures Markets Applied to Prediction (FutureMAP) would the future probability of King Zog I being assassinated be dependent on the amount of money bet on that assassination occurring?

    1. Is that good or bad?
    2. Would knowing that the real Zog survived over 55 assassination attempts change the probability of a future assassination?

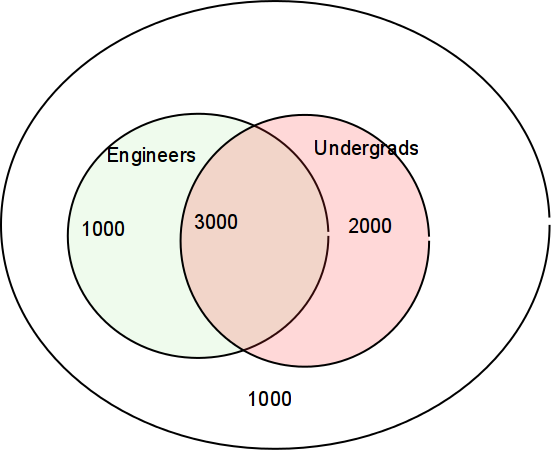
  4. Consider a fictional university that has both undergrads and grads. It also has both Engineers and others:

    /images/venn-stu.png

  5. iClicker: What's the probability that a student is an Engineer?

    1. 1/7
    2. 4/7
    3. 5/7
    4. 3/4
    5. 3/5

  6. iClicker: What's the probability that a student is an Engineer, given that s/he is an undergrad?

    1. 1/7
    2. 4/7
    3. 5/7
    4. 3/4
    5. 3/5

  7. \(P[A\cap B] = P[A|B]P[B] = P[B|A]P[A]\)

  8. Example 2.26 Binary communication. Source transmits 0 with probability (1-p) and 1 with probability p. Receiver errs with probability e. What are probabilities of 4 events?

  9. Total probability theorem

    1. \(B_i\) mutually exclusive events whose union is S
    2. P[A] = P[A \(\cap B_1\) + P[A \(\cap B_2\) + ...
    3. \(P[A] = P[A|B_1]P[B_1]\) \(+ P[A|B_2]P[B_2] + ...\)
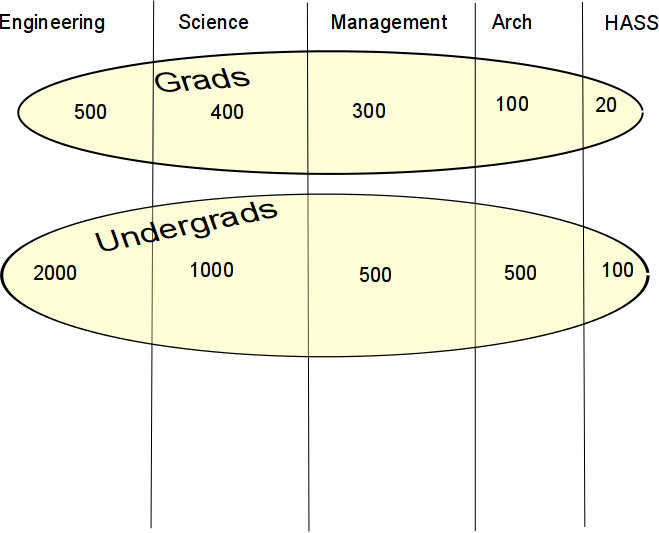
    /images/totalprob.png

    What's the probability that a student is an undergrad, given ... (Numbers are fictitious.)

  10. Example 2.28. Chip quality control.

    1. Each chip is either good or bad.
    2. P[good]=(1-p), P[bad]=p.
    3. If the chip is good: P[still alive at t] = \(e^{-at}\)
    4. If the chip is bad: P[still alive at t] = \(e^{-1000at}\)
    5. What's the probability that a random chip is still alive at t?

  11. 2.4.1, p52. Bayes' rule. This lets you invert the conditional probabilities.

    1. \(B_j\) partition S. That means that
      1. If \(i\ne j\) then \(B_i\cap B_j=\emptyset\) and
      2. \(\bigcup_i B_i = S\)
    2. \(P[B_j|A] = \frac{B_j\cap A}{P[A]}\) \(= \frac{P[A|B_j] P[B_j]}{\sum_k P[A|B_k] P[B_k]}\)
    3. application:
      1. We have a priori probs \(P[B_j]\)
      2. Event A occurs. Knowing that A has happened gives us info that changes the probs.
      3. Compute a posteriori probs \(P[B_j|A]\)

  12. In the above diagram, what's the probability that an undergrad is an engineer?

  13. Example 2.29 comm channel: If receiver sees 1, which input was more probable? (You hope the answer is 1.)

  14. Example 2.30 chip quality control: For example 2.28, how long do we have to burn in chips so that the survivors have a 99% probability of being good? p=0.1, a=1/20000.

  15. Example: False positives in a medical test

    1. T = test for disease was positive; T' = .. negative
    2. D = you have disease; D' = .. don't ..
    3. P[T|D] = .99, P[T' | D'] = .95, P[D] = 0.001
    4. P[D' | T] (false positive) = 0.98 !!!