CG Homework 6, due Mon 2017-10-30 2359 Solution
-
(4 pts) Use the homogeneous matrix to project homogeneous points onto the plane x+3y+2z=4, with COP at the origin. What does the point (1,2,4,5) project to? Give the answer as a Cartesian point.
From https://wrf.ecse.rpi.edu/pmwiki/pmwiki.php/Main/HomogeneousCoords :
Normalize the plane equation to \(x/4 + 3/4 y + 1/2 z = 1\)
The matrix and point vector are \(\begin{pmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 1/4 & 3/4 & 1/2 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 4 \\ 5 \end{pmatrix}\)
Multiply to get \(\begin{pmatrix} 1 \\ 2 \\ 4\\ 15/4 \end{pmatrix}\).
Converted to Cartesian gives \(\begin{pmatrix} 4/15 \\ 8/15 \\ 16/15 \end{pmatrix}\).
You can check that this is on the plane.
-
(4 pts) Repeat the previous question with the COP changed to (1,1,1,1).
The easiest way might be to translate (1,2,4,5) by -(1,1,1,1), project onto the translated plane, then translate the result back.
- Homo (1,2,4,5) is Cart (1/5, 2/5, 4/5).
- The Cart COP is (1,1,1). We will translate everything by (-1,-1,-1).
- (1/5, 2/5, 4/5) translates to (-4/5, -3/5, -1/5).
- The plane equation is changed by replacing x by x+1, y by y+1, z by z+1. (Think about it.)
- x+3y+2z=4 becomes x+3y+2z = -2 becomes -x/2 - 3/2 y - z =1.
- Now multiply \(\begin{pmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ -1/2 & -3/2 & -1 & 0 \end{pmatrix} \begin{pmatrix} -4 \\ -3 \\ -1 \\ 5 \end{pmatrix}\)
- That gives Homo (-4, -3, -1, 15/2) or Cart (-8/15, -6/15, -2/15).
- Translate it back by (1,1,1).
- The answer is (7/15, 9/15, 13/15).
-
(6 pts) Do exercise 5.6 on page 272 of the text.
This is harder than I expected, and so everyone will get full points.
-
(6 pts) This question will take some thinking).
Imagine that you have an infinitely large room illuminated by one infinitely long row of point lights. This figure shows a side view of the room.
The lights are h above the floor and are 1 meter from each other. Assume that the ceiling above the lights is black and that no light reflects off of anything.
An object at distance d from a light gets illuminated with a brightness \(\frac{1}{d^2}\).
Each point on the floor is illuminated by all the lights, but more brightly by the closer lights.
A point p directly below a light will be a little brighter than a point q halfway between two such points. That is the problem --- we want the floor (at least the part directly below the line of lights) to be evenly lit, at least within 1%.
However, the higher the line of lights, the more evenly the floor will be lit.
Your question is to tell us what is the minimum value for h so that the line of the floor below the line of lights is evenly lit within 5%.
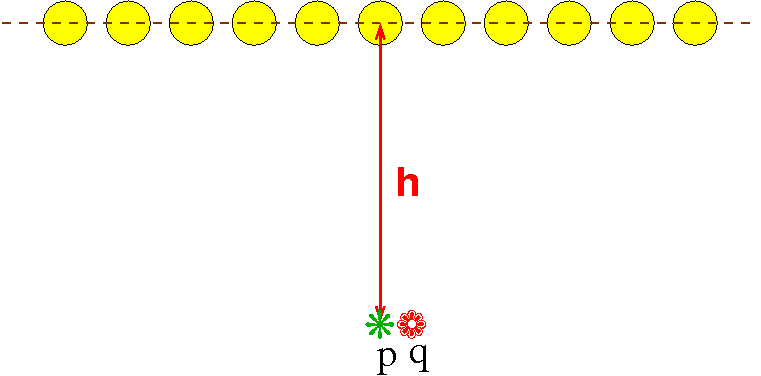
E.g., the brightness at p is
\(b_p = \sum_{i=-\infty}^{\infty} \;\; {1}/{\left(h^2+i^2\right)}\)
Answer:
There are several levels of possible solution, all acceptable. The highest is to find the closed form solutions for the integrals. The lowest is to find the numerical approximation for a specific h by summing 1000 terms, and the plotting the difference as a function of h. Part of the point of this problem is that you have to first decide how to solve it. I will use Mathematica, partly to demonstrate that it is useful in graphics.
The brightness at q is
\(b_q = {\sum_{i=-\infty}^{\infty}} \;\; {1}/{\left(h^2+(i+1/2)^2\right)}\)
From Mathematica, \(b_p = {\pi \coth (\pi h)}/{h}\)
\(b_q = \left({\pi \tanh (\pi h)}/{h}\right)\)
\(b_q/b_p = \tanh ^2(\pi h)\)
The plot is this. The X axis is the height of the lights. The Y axis is the ration between the dimmest place on the floor and the brightest place.
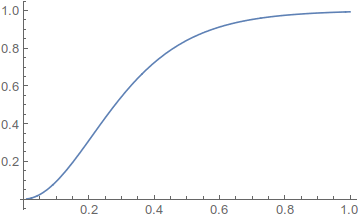
The lesson from this plot is that the light variation smooths out really quickly as the ceiling gets higher. Eyeballing, at h=.7, the variation is already only 5%. Mathematica can calculate 0.69336. Any number from .65 to .75 is acceptable for grading purposes.
(Total: 20 points.)