CG Homework 7, due Thu 2016-10-27 9am
-
(4 pts) Use the homogeneous matrix to project homogeneous points onto the plane x+2y+4z=5, with COP at the origin. What does the point (1,2,4,5) project to? Give the answer as a Cartesian point.
-
(4 pts) Repeat the previous question with the COP changed to (1,1,1,1).
-
(6 pts) Do exercise 5.6 on page 272 of the text,
-
(6 pts) This question will take some thinking).
Imagine that you have an infinitely large room illuminated by one infinitely long row of point lights. This figure shows a side view of the room.
The lights are h above the floor and are 1 meter from each other. Assume that the ceiling above the lights is black and that no light reflects off of anything.
An object at distance d from a light gets illuminated with a brightness \(\frac{1}{d^2}\).
Each point on the floor is illuminated by all the lights, but more brightly by the closer lights.
A point p directly below a light will be a little brighter than a point q halfway between two such points. That is the problem --- we want the floor (at least the part directly below the line of lights) to be evenly lit, at least within 1%.
However, the higher the line of lights, the more evenly the floor will be lit.
Your question is to tell us what is the minimum value for h so that the line of the floor below the line of lights is evenly lit within 1%.
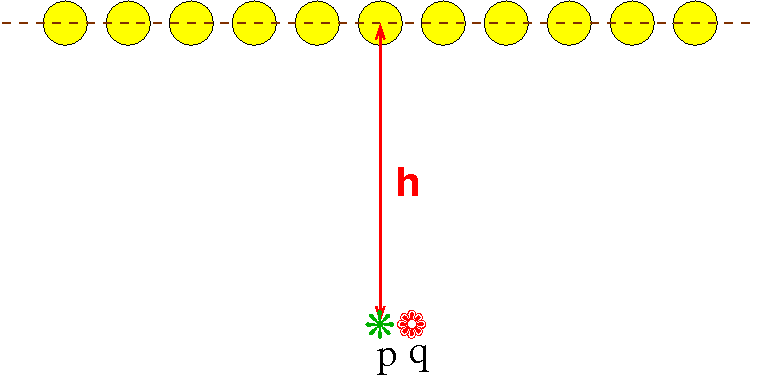
E.g., the brightness at p is
\(\sum_{i=-\infty}^{\infty} \;\;\; \frac{1}{h^2+i^2}\)
(Total: 20 points.)