This document is a vision statement for future research in computational and geometric cartography. This is one component of the new NSF/DARPA joint solicitation in Computational Algorithms and Representations for Geometric Objects (CARGO). Other components include computational topology and computer aided design.
Terrain (elevation) data have complicated, long range, nonlinear, relationships, such as drainage networks. Data structures and operations like compression that ignore this will be suboptimal, and often erroneous. The data may have several related layers, whose internal consistency must be maintained. Important terrain applications include visibility determination and mobility calculation. Since the input data are imprecise, determination of the output accuracy, and "just good enough" computation are important, in order to obtain the most, valid, results in the least time. The techniques developed may then be useful in geology. The inherent nonlinearity of the problem may inspire new applied mathematics.
The proposed research is quite at variance with traditional GIS, as that field defines itself. This work will require serious mathematical and computer science expertise, applied to the largest available real datasets to solve applications in the nonideal Galilean, not Aristotelian, real world. It is appropriately performed in the Numeric, Symbolic, and Geometric Computation and Program, together with Mathematics.
The major problem, and opportunity, in Computational and Geometric Cartography is the complex of long range, non-linear, elevation data relationships. For example, rivers such as the Amazon extend from one coast almost to the other side of the continent. Terrain also has many more local maxima than minima. Terrain above sea level is statistically different from the sea floor. Earth terrain is different from lunar terrain. Elevation, considered as a scalar field, is not always differentiable, or even continuous. Real terrain is more irregular than databases such as DEM-1 cells.
Traditional, linear, geostatistical models such as kriging do not capture this complexity. Fractal terrain models are also quite unrealistic.
User quality metrics are also nonlinear. While simple metrics like RMS error are generally adequate in the image processing community, they are too simple for terrain, for many reasons such as these.
When lossily compressing terrain, preserving features like gullies may be more important than maintaining exact elevations.
Because real terrain, except for karst territory and deserts, has few local minima, the stored terrain shouldn't. Note that DEM-1 data does not nearly satisfy this property, indeed has so many that finding drainage patterns is considerably harder.
Preserving derived properties like drainage and visibility is more important than minimizing elevation error.
For efficiency and accuracy reasons, the data may be represented in several layers, such as elevation and slope. Preserving their mutual consistency may be more important than accuracy. For example, if two layers are elevation and hydrography, it is desirable that, after restoration, contour lines shall continue to be perpendicular to rivers, and shall not cross shorelines. This requirement is not met by some current commercial mapping packages. Here are two sample maps generated by Delorme TopoUSA.
This first map shows a stream that is crossing contour lines obliquely, which is physically impossible. The river layer and the elevation layer were apparently lossily compressed separately. When restored, they are inconsistent with each other.
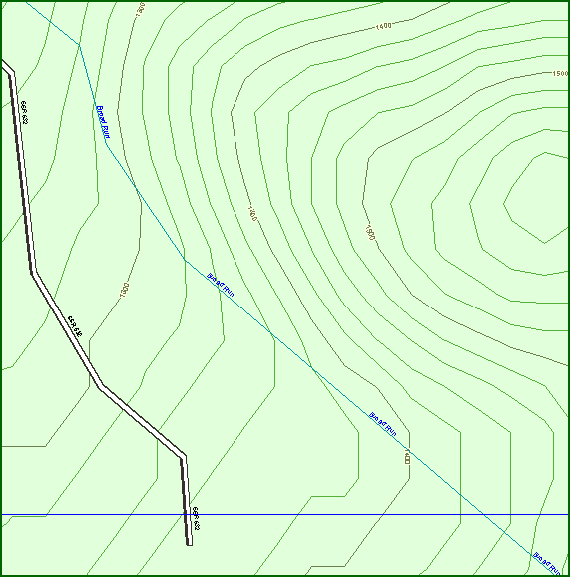
Commercial Mapping Product Showing Stream Crossing Contour Obliquely
The second map shows contour lines crossing into a lake, which is also impossible.
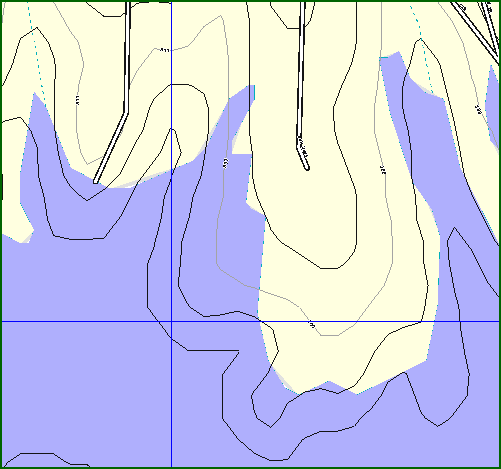
Commercial Mapping Product Showing Contour Lines Crossing Lake Shoreline
The problem of these complex terrain interrelationships provides an opportunity for considerable research, to be described next.
(top)This section lists several research topics in Computational and Geometric Cartography, of varying depth and difficulty.
3.1. The Appropriate Data Structure
The question of the proper representation of terrain elevation data is still open. The major competitors are Triangulated Irregular Networks (TINs), first implemented in cartography by Franklin in 1973, and regular arrays (grids) of elevations, such as the USGS Digital Elevation Model (DEM). It is not yet clear which method is better.
Elevation arrays are much more compact and easier to work with. However, the array's resolution is inherent in the data structure, and the earth's curvature also presents problems.
Either technique may be made hierarchical, although a hierarchical TIN is a rather complex. Compact representations for the TIN topology are now available, so that the topology no longer requires ten times the storage that the geometry does.
Using the simplest possible data structures is advantageous since they are easier to debug, which leaves time for understanding and tuning the implementations. Frequently, they are also simultaneously smaller and faster.
If TINs are chosen, then there are several unanswered research questions, such as the following.
How does error correlate to number of triangles?
Is a Delauney triangulation the best, or merely the most popular and easiest to analyze?
-
What is the best method of selecting points? The two opposite methods are these: (1) insertion of points into an initial minimal triangulation, and (2) initially triangulating all the points, followed decimation, or deletion of the least useful ones. Perhaps we should alternate inserting and deleting points, as is done in a stepwise multiple linear regression.
One oft-mentioned strategy is to a conduct a constrained triangulation, which forces points on features like ridge lines, to be included. Is it really better, or it is another of those ideas that are more obvious than good?
On the other hand, if the triangulation automatically includes such features, then do we have a useful feature-detection algorithm?
-
How should curved surfaces, such as triangular spline patches, be added to the TIN? The simplest method could go as follows.
-
Find a planar TIN for the data.
-
Fit triangular splines to the triangles, while maintaining the highest continuity possible across the edges.
-
Measure the error. If the terrain generally is C2, albeit with exceptions (as described above), then the error should be less, even though no information was added by fitting the splines to existing triangulation.
(There is a precedent for this form of behavior. A Taylor or Chebyshev polynomial approximation to a function may be formally transformed to a rational (Pade) form. This is a transformation of the polynomial, w/o reference back to the original function being approximated. Nevertheless, the resulting Pade approximation is often more accurate than the Taylor or Chebyshev approximation that it was created from. By conservation of information, there must also be functions whose approximations get worse. However, they tend not to be the functions that people want to approximate.)
-
The next level of sophistication is to choose the triangular splines so as to minimize the error. This process is theoretically difficult, and not yet fully reduced to a black box. Therefore, the payoff will be the greater.
-
Real terrain tends to have continuous patches separated by discontinuities (cliffs). As this form of approximatation seems relatively untouched, even theoretically, there is a need for serious mathematics.
The above questions may seem to be mere implementation details. However, they want to be settled first, since the answers affect all future research in the project. E.g., a visibility program on an elevation array shares little code with a visibility program on a TIN.
3.2. A General Model of Terrain
Better terrain models would enable a theoretical analysis, from first principles, of the performance of any proposed compression, visibility, drainage, or other terrain algorithm. We could ask questions such as, "what is the theoretically best compression algorithm preserving certain properties?" Two possible strategies here are as follows.
A shallow model attempts to recapture the surface's behavior w/o knowing any geology. Both the autocorrelation and fractal methods are like this. Shallow models can work: we model people's height and weight statistically as normal distributions w/o knowing any physiology. However, the nonlinear correlations described in an earlier section would seem hard to model simplistically.
Much work has been done on theoretically modeling surfaces, e.g., with autocorrelations or fractals. They might eventually be made to generate realistic surfaces if enough parameters were added. (The Ptolemaic model of planetary orbits was initially more accurate than Kepler's, because the Ptolemaic system had so many epicycles, like terms in a Taylor series.)
On the other hand, a deep model recaptures the processes by which surfaces are formed, such as erosion and orogeny. Water erosion is especially important since it is the major creative force for terrestrial terrain. This does not apply to the moon, to Jupiter's moons, or to Venus, data for which is becoming increasingly available. Since those surfaces' terrains should be statistically different, the resulting impact on the speed and output distribution of our algorithms and data structures merits study.
A conceptually deeper representation, based on a basis set of geomorphological forces that created the terrain, such as uplift and downcut, might be possible. Then we might deduce the operators that created this particular terrain, and store them. This approach is quite successful in mathematics, where various different sets of basis functions, each with particular strengths, are used. They include sin and cos functions used in Fourier transforms, square wave functions used in Walsh transforms, and arccos functions used in Chebyshev approximations. While all the above basis sets can also be used in a shallow terrain representation, the hope is that exploiting the richer structure of geomorphology will lead to more economical representations, if the difficulty that geomorphological operators are nonlinear can be overcome.
Finally, can the classic idea of representing the terrain by the features that people would use to describe it be made workable? The problem is that we can't just say that there is a hill over there, it is necessary to specify the hill in considerable detail. That might take more space than simply listing all the elevations with a grid or TIN. There is also the danger that this idea is more attractive than it is good.
3.3. Compression
3.3.1. Introduction
The large, and growing, volume of terrain data requires effective compression, which may be either lossless or lossy. For terrain data, of limited accuracy, lossy compression is appropriate, since it is sufficiently accurate and produces much smaller compressed files. Many lossy compression techniques contain the very useful progressive resolution and progressive transmission properties. This means that a low resolution, high error, database is transmitted first, and then followed by corrections to improve its resolution or accuracy. This does not necessarily require sending any more bits in total than would be required by sending the desired accurate database all at once.
3.3.2. Evaluation
The simplest error metric for a lossy compression of a single layer of terrain data, elevation, would be a function of the elevation error, such as RMS or maximum. However, since the data is being compressed in order to later use it in some application, more sophisticated metrics are desirable. They would include a determination of how derived properties, such as drainage patterns or the location of the most visible points change. If these are robust with respect to elevation errors, then a lossier compression, resulting in smaller files, would be acceptable.
3.3.3. Effect of Data Structure Choice
The choice of data structure controls the possible compression methods. For example, wavelet compression methods can apply to an elevation array, building on their success in compressing photographic images. Although their error metrics are considerably different, so much effort has been devoted to optimizing wavelet compression techniques, that they serendipitously also compress terrain data tolerably well. This indicates that wavelet basis functions that were designed specifically for terrain might perform even better. Nevertheless, wavelets have two major problems. First, since the whole point of wavelets is their finite support, i.e., a wavelet basis function is nonzero over only a small region, it might be harder to use them to model the long range data dependencies described earlier. Second, wavelets have been researched so thoroughly in the last five years that revolutionary advances may be less likely.
If the TIN format is used instead, then a hierarchical TIN is possible. This is complicated since the triangles at one level generally cut across the triangles at the lower level. In computer graphics, the recent concept of Levels of Detail has received considerable attention for progressively transmitting triangulated 3-D objects. It should be tested against, and adapted for, terrain.
3.3.4. Are Hierarchies Always Necessary?
Since the data accuracy varies, it's obvious and almost universally accepted that the data structure should be hierarchical. This may not always be correct. A flat data structure is so much simpler, which means that it is smaller, faster, easier to debug, easier to implement on a parallel machine, and thrashes a cache or virtual memory manager less. Consider how these advantages reinforce each other. A smaller data structure means that more elements fit into the cache, so there are fewer cache misses. They also take less time to transmit on an I/O limited system, which is most systems.
One example of a flat data structure handling uneven data is the use of Franklin's uniform grid to find edge intersections, when the edges are roads from a Digital Line Graph that contains both urban and rural areas. The algorithm superimposes a uniform grid on the map, sorts the edges into cells, and pairwise tests all edges that fall into the same cell. Although some cells may have ten times the average number of edges, both statistical analysis and implementation experience demonstrate that this method is extremely fast.
Finally, some hierarchies, such as quadtrees, in fact, cannot process very uneven data, because they would require so many levels that they would be worse than a flat data structure.
3.3.5. Compressing Multiple Layer Data
We often have a database containing separate layers of information, such as both coastline and elevation, or both elevation and slope, or both contours and rivers. These layers are correlated with each other. E.g., rivers should cross contours perpendicularly.
Note that we might want to store a layer explicitly even when it can apparently be derived from another layer. For example, the slope is the magnitude of elevation's derivative. However taking the derivative increases any errors, and some decisions, such determining whether a helicopter can land and also take off, are sensitive to the slope.
One difficult but important problem is how to lossily compress this database, while maintaining internal consistency. If the layers are compressed separately, they will be inconsistent when restored; see the examples above.
This idea can be generalized to include other desirable data restrictions. For instance, when reconstructing a surface, not creating or destroying gulleys, which may affect mobility, and in which people may hide, may be more important than minimizing the RMS error.
3.4. Terrain visibility
3.4.1. Definitions
Consider a terrain elevation database, and an observer, O, who is looking for targets on the terrain. The observer might be situated on a tower at a certain height above the terrain, looking for targets also flying at a certain height, which are represented by the point directly below on the terrain. The viewshed is the terrain visible from O within some distance R of O. The visibility index is the area of the viewshed.
The following figure shows a viewshed with error bars for a region in northeastern New York State. The observer on Mt Marcy is marked by a white square near the lower left.

Sample viewshed output
The elevation of the possible visible targets is indicated by colors. The probability that a particular target is visible is indicated as follows.
- Unshaded (
 ): almost certainly visible.
): almost certainly visible.
- Lightly shaded (
 ): probably visible.
): probably visible.
- Darkly shaded (
 ): probably hidden.
): probably hidden.
- Black (
 ): almost certainly hidden.
): almost certainly hidden.
The following example shows visibility indices. The first image shows some sample terrain from South Korea, color-coded by elevation, while the second shows the colod-coded visibility indices of the points, for a particular observer and target height and radius of interest.
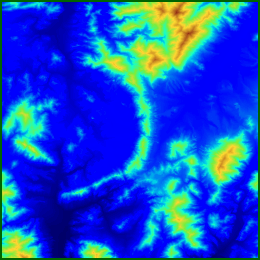

Sample Terrain; Visibility Indices
Visibility indices can be counterintuitive; the following scatterplot of a random sample of points from the above map demonstrates the sometimes small relation of height to visibility. In this example, the correlation is slightly negative, although statistically insignificant.
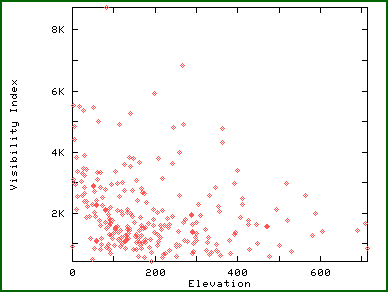
Elevation vs Visibility Index
The viewshed may be computed for a fixed observer on an elevation array by running lines of sight from the observer to the targets on the perimeter of Region of Interest (ROI). As each perimeter target's visibility is determined, the visibilities of all closer points along the line of sight are also calculated. The entire process executes in time linear in the number of targets. Processing 1201x1201 level-1 DEMs is easy.
The visibility indices of all possible observers are efficiently computed by randomly sampling perhaps 100 potential targets for each observer.
3.4.2. Complexity Reduction
Visibility, as we've presented it, is affected by several parameters in addition to the actual terrain: the observer height, the target height, the radius of interest, and the number of sample targets per observer. These parameters' effect need to be studied, with a view to discovering generalizations to reduce the number of test cases needed to test new visibility algorithms.
Here's an example. Increasing the observer and target heights acts to blur the terrain so that fine details are less important. This means that lower resolution data could suffice here.
3.4.3. Applications and Extensions
Terrain visibility determination is a rich topic, with many applications and extensions. Siting radio transmitters is only the most obvious possibility. Conversely, locating points at which to hide, from optimally placed observers, may be desirable. For example, a timber company may want a forest clearcut to be invisible to observers driving on a highway that itself was sited to give a good view. This begins to be reminiscent of game theory.
In order the best to place observers, the visibility indices of the complete map are unnecessary; we need to know only what the most visible points are. Here, statistical sampling techniques from production quality control in industrial engineering are useful. An initial estimate of a particular observer's visibility index might be calculated from a small number of random targets. Only if this initial estimate is high enough, might we test more targets to refine the estimated visibility index, to decide whether or not to use this observer.
Instead of placing one observer, it may be desirable to optimize the locations of several observers so that they jointly cover the whole terrain. To accomplish this, a viewshed algorithm and a visibility index algorithm can be alternated. The visibility index algorithm will produce the most visible point, its viewshed can be found, then the most visible point not in that viewshed can be determined, and so on.
It might also be required that each possible target be seen by at least two observers.
The set of observers might be fine-tuned with a technique reminiscent of a multiple stepwise linear regression with independent variable addition and deletion. Efficiently calculating areas of sets of intersecting and uniting polygons is required to make this feasible. That is a solved problem.
Instead of minimizing the set of observers, a more sophisticated cost function is possible, which recognizes that one higher, and more expensive, observer may be as useful as two lower and cheaper ones. The cost of placing an observer may even depend on whether other observers are nearby, when placing the observer requires building a road.
The ultimate goal may be a fully automatic system for siting observers (or potential targets). A valuable intermediate goal could be a software terrain assistant, to help the human planner by calculating viewsheds for situations that the human inputs. This assistant must be fast enough, ideally less than a second per test, for the human planner to rapidly test many scenarios to find the optimum. The human should even be able to draw a trajectory for a moving observer, and see a video of the changing viewshed. Apart from the specific visibility results obtained, this will enable the human will develop a better intuition of how visibility works.
Finally, if determining terrain features like ridge lines is desirable for another application, then visibility may help. Many of the most visible points seem to run along the ridges. (How this can be true simultaneously with higher points not necessarily being more visible requires thinking.) If all the elevations are negated before determining visibility, then the valleys may result.
3.4.4. Hierarchical Visibility Computation
A hierarchical data structure should allow more accurate visibilities to be determined more quickly. Indeed, when running a line of sight to some distance from the observer, it is desirable to test the line against larger sections of the terrain.
3.4.5. Error Bounds
Establishing error bounds on output as a function of approximations in the algorithm and uncertainties in the data is critical. For example any visibility algorithm on a DEM must decide how to interpolate elevations when a line of sight passes through a point between two adjacent posts. Indeed, the grey areas of the above Sample viewshed output figure above, which cover half of the whole map, were obtained merely by varying the elevation interpolation algorithm for such points. This says that we really do not know the visibility for half of the map (for this choice of observer, and observer height, etc).
Therefore, we should be asking more generalized questions, such as these.
-
When this algorithm is used to site an observer, what are the odds that he will have blind spots that we didn't calculate?
-
What will it cost to place observers to guarantee that there will be no blindspots?
-
How does this depend on the terrain type, and on the observer height etc?
-
What is the tradeoff between data quality and this cost?
3.5. Just Good Enough Computation
How can we turn this input uncertainty and output sensitivity to our advantage? Precise calculations are not warranted here, just as carrying many significant digits is not always warranted in a physics calculation.
This apparent problem is, rather, an opportunity, to design faster, just accurate enough, algorithms, that extract all the information, but no more, from the data. A sufficient quantitative speedup will enable a qualitative growth in the set of solvable problems, perhaps including the intervisibility problem defined earlier.
3.6. Mobility
Consider a database of terrain elevation and ground conditions, such as soil type and tree stem size. The problem is to determine the best feasible route for a hiker, truck, or tank from point A to B. We must avoid the temptation to make the problem unrealistic while simplifying it enough to solve it. Battles have been won, such as in the Ardennes forest in 1940, when one side traversed an area that the other side thought was impassable.
The simplest mathematical formulation of this is as a shortest path graph traversal problem, perhaps using a Dijkstra algorithm, although if the roads have capacity limits the situation is more complicated. Then there are the transportation capacity paradoxes, where adding a new road increases every driver's delay, if each driver independently chooses the quickest route.
However, idealizing a mobility problem to use classical graph theory is probably unrealistic. In the real world, travel occurs overland, across terrain. Capacity limits are gradual and complicated. E.g., driving on a highway shoulder, albeit at a slower speed, may be possible. North-south traffic through an intersection interferes with east-west traffic. Driving on dirt roads wears them out, at a speed depending on the weather. Any mobility program that ignores these is pointless. Nevertheless, since people now can route forces w/o computer assistance, progress must be possible, if only to design a computerized mobility assistant for the human planner.
The recent intervisibility problem concerns planning the joint mobility of a group. Assume that a platoon of soldiers wishes to move from A to B, having regard to the considerations described above, plus two new constraints. First, the soldiers wish to remain pairwise visible to each other in order to communicate via VHF radio. Second, the soldiers wish to remain dispersed so that there is never a possible single other observer who can simultaneously see them all.
3.7. Determining Drainage Networks
Techniques useful for the above applications will also provide faster ways to determine what drainage networks would form on a given terrain. This problem links back to the question of an appropriate data structure, as follows. Real terrain, as mentioned, has few local minima. However, if the elevation is measured on only a regular array of posts, then that array will have local minima when the drainage channel fits completely between two adjacent posts. The problem can apparently be corrected by changing the elevations of these locally minimal points. (That's harder than it sounds. Indeed, since often the low region is several points large, a simple median filter is insufficient.) However, since adding deliberate errors is ugly, what might be a better data structure, which preserves the property of no local minima?
3.8. Geological Data Structures
Experience from computational and geometric cartography may help us to develop three-dimensional data structures and algorithms in geology, in spite of the fact that geometry in 2D differs from 3D in several respects, of which the following is only a small sample.
A 2D Voronoi diagram on N points has a linear number of edges, while a 3D Voronoi diagram on N points may easily have N2/4 faces.
-
Every point inside a polygon is visible from at least one vertex. However, some polyhedra have interior points hidden from all that polyhedron's vertices.
There are an infinite number of regular polygons, but only 5 (or 9, depending on definitions) regular polyhedra.
A square can be partitioned into smaller squares, all different sizes. A cube cannot be partitioned into smaller cubes of different sizes.
-
All (2D) polygons are decomposable into triangles by adding only interior edges, while not all (3D) polyhedra are decomposable into tetrahedra by adding only interior faces.
-
Finally, for polygons, all such decompositions have the same number of triangles, while some polyhedra can be decomposed different ways into different numbers of tetrahedra.
There has been considerable work in modeling various processes such as erosion. However, the researchers have been more geologists than computer scientists. A project building on this work, using skills serious computer scientist and mathematical skills might have large payoffs.
3.9. The Unreasonable Effectiveness of Heuristics
An open theoretical issue is why some simple algorithms, which have intolerable worst-case times, work so well in practice. Edge segment intersection and visible surface determination with a uniform grid are examples. What does in practice mean? It's unfairly optimistic to assume the data to be uniform and uncorrelated, but unfairly pessimistic to make no assumptions at all. Most analytical cartography implementations that everyone uses every day can be made to fail by an adversary who selects the worst possible input.
We tolerate that because we work in the real world, not the theoretical world of worst-case algorithms analysis. Nevertheless, a theoretical characterization of these algorithms might enable them to perform better in the real world.
3.10. Nonlinear Mathematics
Mathematical approximation theory prefers to use linear functions when possible. The availability of an easily characterized set of basis functions, which can be linearly combined, is quite advantageous. Nevertheless, nonlinear approximations, such as rational functions, can be more efficient. Functions like absolute value and the step function do not have uniform polynomial approximations, but have good rational approximations. Even for smooth functions like exponential, the best rational approximation is more efficient than the best polynomial one. The cost is in the difficulty of finding the rational approximation. The routines to find the approximation are not as available, and are slower to execute.
Given the major application area of Computational and Geometric Cartography, more research into nonlinear approximations and representations is desirable.
(top)Absent a theoretical model of terrain, competing algorithms and data structures must be evaluated by testing on sample datasets. One danger is that available data may be statistically different from the real world, principally by being smoother. This makes the data to be less noisy and more compressible, and to have fewer local extrema. That raises a serious question of whether an algorithm that works well on, say level-1 DEMs, would still work on more accurate data. Also, since elevation arrays depend on the grid, it's possible that different grids might perform differently.
(top)5.1. Striking a New Direction
Our proposed research is not Geographic Information Science (GIS), as that community defines itself, but strikes in a new direction. The deep and strategic issues in GIS, as determined by the community, most recently expressed at the final session of the recent GIScience 2000 conference in Savannah, are ontological. How should we organize spatial information? What does it all mean? Leaders in the community have pondered these important questions for millenia; Aristotle was frequently cited at GIScience 2000. We would not presume to contribute here.
Instead, we feel that GIS is hampered by this Aristotelian approach, which attempts to create an ideal organization of cartographical knowledge in the abstract. Half a millenium ago, this approach blocked any advance in astronomy. Aristotelians disbelieved Galileo's observations of the imperfect, complicated, nature of the real world, such as sunspots. The current analogue to Galileo's observations is our observing the results of computer experiments. When operating on terrain data, we also observe unexpected, complicated, phenomena. One example is that higher points are not always more visible. This experimentation to determine how things are is more important than thinking about how things should be. The ultimate goal is, as it was with the astronomers, to synthesize new theory to explain why the world is as it is.
It's obvious that terrain features like ridges should be forced into the data structure. It's obvious that all data structures should be hierarchical. It's obvious that higher points are more visible than lower ones. However, none of these obvious truths may necessarily be true. Experimentation is required, which will sometimes also lead us in new directions.
Because of the nonlinearity of real terrain, traditional linear methods like kriging may not be appropriate. The use of nonlinear algorithms is another new direction for this research.
5.2. Fit Within NSF
This proposed research is Computational Geometry, as applied to computational and geometric cartography. Computational Geometry is one of the subareas of NSF's Numeric, Symbolic, and Geometric Computation (NSG) Program, which I manage, in the Division of Computer-Communications Research (C-CR), in the Directorate for Computer and Information Sciences & Engineering (CISE). Computational Geometry develops and implements geometric theory on computers.
This research might appear to be geographic in nature, and relevant to the Geography and Regional Sciences program in the Division of Behavioral and Cognitive Sciences, in the Directorate for Social, Behavioral, and Economic Sciences. However, that program, in accord with the GIS community, is tasked with enhancing geographical knowledge, concepts, theories, and their application to societal problems and concerns, http://www.nsf.gov/sbe/bcs/geograph/start.htm) In contrast, this proposed work has no societal component, and so is irrelevant to GRS.
In the Numeric, Symbolic, and Geometric Computation Program, previous Computational Geometry applications have included motion planning in robotics, clothing piece layout, and protein folding. This current proposed research continues in this successful methodology.
5.3. Fitting the Pieces Together
The following chart shows how the pieces fit together.
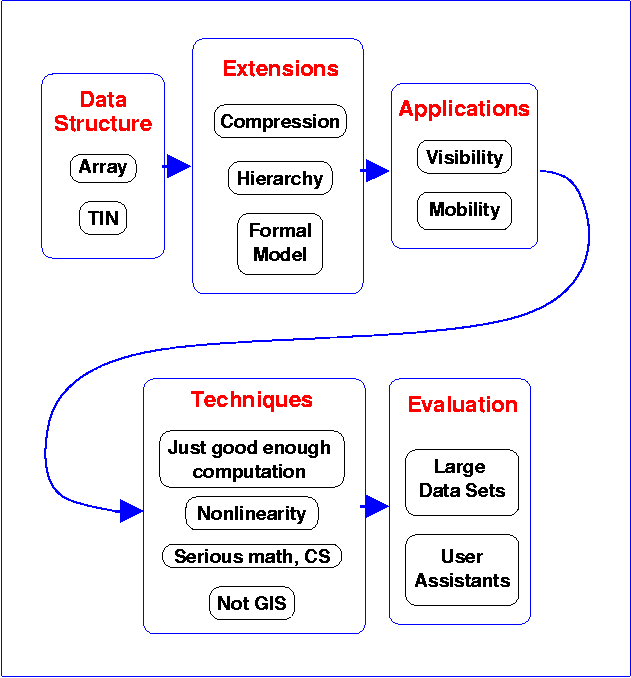
Fitting the Pieces Together
This work has the potential to set the direction of research in the profession for many years to come. The large datasets are here. The computational power is available. Users with pulls demand that their applications be solved. Deep math techniques and strong CS skills are available. The only lack is that, no one has put the pieces together until now. We can do that.