1. (4 pts) Use the homogeneous matrix to project homogeneous points onto the plane 2x+3y+4z=5, with COP at the origin. What does the point (1,2,4,5) project to? Give the answer as a Cartesian point.

   Use https://wrf.ecse.rpi.edu/pmwiki/Main/HomogeneousCoords

   The plane is 2/5 x + 3/5 y + 4/5 z = 1. The matrix is

   \(M=\begin{pmatrix} 1 &0&0&0\\ 0&1&0&0\\ 0&0&1&0 \\ 2/5 &3/5&4/5&0 \end{pmatrix} =\begin{pmatrix} 5 &0&0&0\\ 0&5&0&0\\ 0&0&5&0 \\ 2 &3&4&0 \end{pmatrix}\)

   \(p_h'=\begin{pmatrix} 5 &0&0&0\\ 0&5&0&0\\ 0&0&5&0 \\ 2 &3&4&0 \end{pmatrix} \begin{pmatrix} 1\\2\\4\\5\end{pmatrix} = \begin{pmatrix} 5\\10\\20\\24\end{pmatrix} \implies p_c = \begin{pmatrix} 5/24 \\10/24 \\20/24 \end{pmatrix}\)

2. (4 pts) Repeat the previous question with the COP changed to (1,1,1,1).

   The easy way is to translate \(p_c = (1/5, 2/5, 4/5)\) by (-1,-1,-1) to \(q_c=(-4/5, -3/5, -1/5), q_h=(4,3,1,-5)\), project to \(q_h'=(20,15,5,21). q_c'=(20/21, 15/21, 5/21)\), then translate the result by (1,1,1) to get (41/21, 36/21, 26/21).

3. (6 pts) Do exercise 5.6 on page 272 of the text,

   This looks for the general solution to the previous question.

   Multiply the matrices to translate, project, and translate back.

   If the projection plane is ax+by+cz=1 and the center of projection is (d,e,f), then (if I did this right; I multiplied the matrices with Mathematica) the homogeneous projection matrix is

   \(\begin{pmatrix} 1+a d & b d & c d & -d (1+a d)-b d e-c d f\\ a e & 1+b e & c e & -a d e-e (1+b e)-c e f\\ a f & b f & 1+c f & -a d f-b e f-f (1+c f)\\ a & b & c & -a d-b e-c f \end{pmatrix}\)

4. (6 pts) This question will take some thinking).

   Imagine that you have an infinitely large room illuminated by one infinitely long row of point lights. This figure shows a side view of the room.

   The lights are h above the floor and are 1 meter from each other. Assume that the ceiling above the lights is black and that no light reflects off of anything.

   An object at distance d from a light gets illuminated with a brightness \(\frac{1}{d^2}\).

   Each point on the floor is illuminated by all the lights, but more brightly by the closer lights.

   A point p directly below a light will be a little brighter than a point q halfway between two such points. That is the problem --- we want the floor (at least the part directly below the line of lights) to be evenly lit, at least within 1%.

   However, the higher the line of lights, the more evenly the floor will be lit.

   Your question is to tell us what is the minimum value for h so that the line of the floor below the line of lights is evenly lit within 10%.

   

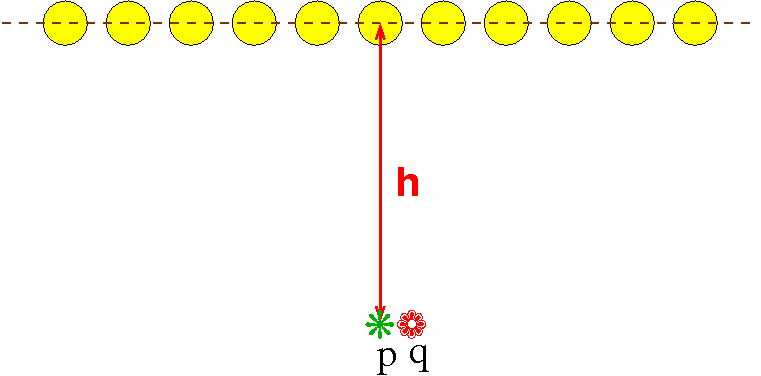
   E.g., the brightness at p is

   \(b_p=\sum_{i=-\infty}^{\infty} \;\; \frac{1}{\left(h^2+i^2\right)}\)

   There are various acceptable ways to solve this. Here is one.

   The brightness at q is

   \(b_q=\sum_{i=-\infty}^{\infty} \;\; \frac{1}{\left(h^2+(i+1/2)^2\right)}\)

   \(b_p = \pi \coth(\pi h)/h, b_q = \pi \tanh(\pi h)/h\)

   \(b_p / b_q = \tanh^2(\pi h) = .9\)

   \(\pi h = 1.818413, h = 0.5788\)

   Another way, if you don't know how to sum the formulae is to write a function to compute \(b_p/b_q\) numerically as a function of h (sum 1000 terms), plot it and look for the value of h.

(Total: 20 points.)