Geometric Operations on Millions of Objects
Wm Randolph
Franklin
Rensselaer Polytechnic Institute
http://wrfranklin.org/
Research Context
- (Blue sky:)
Geologically correct terrain representation
- Soon to be DARPA/DSO/Geo* sponsored (via NGA).
- Replace Fourier series, fractals with scooping and other nonlinear operators that respect how terrain is formed.
- (Applications) to geometry and cartography
- e.g., multiple observer siting with intervisibility on terrain
- Efficient fundamental operations, like finding nearest neighboring points, finding connected components, etc.
- A proper foundation is necessary for the blue sky projects' success.
Today: How to process large geometric databases quickly!
What?
- Larger and larger geometric databases are available, with tens of millions of primitive components.
- We want to perform geometric operations, such as
- interference detection
- boolean operations: intersection, union
- planar graph overlay
- mass property computation of the results of some boolean operation
- Apps:
- Find the volume of an object defined as the union of many overlapping primitives.
- Two object interfere iff the volume of their union is positive.
Themes
- Limited address space => must minimize storage => I/O is faster.
- For N>>1,000,000 lg N is nontrivial => deprecate binary trees
- Minimize explicit topology, expecially in 3D.
- Plan for 3D; many 2D data structures do not easily extend
to 3D.
- 2D line sweep easily finds intersecting edge segments.
3D plane sweep would need to maintain a planar graph of the active faces. Messy!
- 2D Voronoi diagram is useful.
However space for 3D Voronoi diagram is easily O(N2).
Confessions
- I'm not necessarily a deep philosophical thinker because
I'm always seeing holes in the generalities. I like Galileo
better than Aristotle. Galileo experimented.
- I try to do small things well, to lay a foundation of
computational observations and tools on which to generalize.
- This is driven by a deep knowledge of classical geometry,
where the order is implicit in the axioms. You don't need to
store it explicitly to use it.
- Example of hidden order: the centroid,
circumcenter, and orthocenter of a triangle
are collinear.
- Yes, the above points are a little contradictory.
Theme: Minimum Explicit Topology
- What explicit info does the application need? Less > simpler
- Object: polygon with multiple nested components and holes.

- Apps:
- area
- inclusion testing.
- Complete topology: loops of edges; the tree of component containments.
- Necessary info: the set of oriented edges.
Point Inclusion Testing on a Set of Edges
- "Jordan curve" method
- Extend a semi-infinite ray.
- Count intersections.
- Odd <==> Inside
- Obvious but bad alternative: summing the subtended angles.
Implementing it w/o actually doing arctan to compute
the angles, and handling special cases wrapping around 2pi
is rather tricky. Then it reduces to the Jordan curve
method.
Area Computation on a Set of Edges
- Each edge, with the origin, defines a triangle.
- Sum their signed areas.
Advantages of the Set of Edges Data Structure
- It's simple enough to debug.
SW can be simple enough that there are obviously no errors, or complex enough that there are no obvious errors.
- It takes less space to store.
- Parallelizing is easy.
- Partition the edges among the processors.
- Each processor counts intersections or sums areas independently, to produce one subtotal.
- Total the subtotals.
What About a Set of Vertices Data Structure?

- Too simple.
- Ambiguous: two distinct polygons may have the same set of edges.
Set of Vertex-Edge Incidences
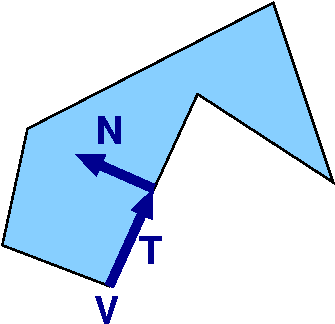
Here's another minimal data structure.
The only data type is the incidence of an edge and a vertex, and
its neighborhood. For each such:
- V = coord of vertex
- T = unit tangent vector along the edge
- N = unit vector normal to T pointing into the polygon.
Polygon: {(V, T, N)} (2 tuples per vertex)
Perimeter = - (V.T).
(V.T).
Area = 1/2  ( V.T V.N )
( V.T V.N )
Multiple nested components ok.
Demonstration: Mass Properties of the Union of Millions of Cubes

Demonstration: Mass Properties of the Union of Millions of Cubes

- This illustrates the above ideas.
- This is a prototype on an easy subcase (congruent axis-aligned cubes).
- The ideas extend to general polyhedra.
- This is not a statistical sampling method - the output is exact, apart from losing 15 significant digits during the computation.
- This is not a subdivision-into-voxel method - the cubes' coordinates can be any representable numbers.
Goal
- Given millions of overlapping polyhedra:
- compute area, volume,
etc, of the union.
- This does not require first computing the explicit union polyhedron.
- The computation is exact.
- Apps: swept volumes, interference detection, etc.
- We present a prototype implementation for identical cubes.
- (However: The theory is general.)
- Tested to: 20M cubes.
- Possible extensions: interference detection between two
objects, each a union of many primitives; an online algorithm,
with input presented incrementally; deletions.
Application: Cutting Tool Path

- Represent path of a tool as piecewise line.
- Each piece sweeps a polyhedron.
- Volume of material removed is (approx) volume of union of those polyhedra.
- Image is from Surfware Inc's Surfcam website.
Traditional N-Polygon Union

- Construct pairwise unions of primitives.
Iterate.
- Time depends on assumed size of intermediates, and assumed
elementary intersection time.
- Let P = size of union of an M-gon and an N-gon. Then
P=O(MN).
- Time for union (using line sweep) T=
 (P lg P) .
(P lg P) .
- Total T=O(N2lg N).
- Hard to parallelize upper levels of computation tree.
Problems With Traditional Method
- lg N levels in computation tree cause lg
N factor in execution time. If N>20, that's
significant.
- Intermediate swell: gets worse as overlap is worse. Intermediate computations may be much larger than the final result.

The explicit volume has a complicated topology:
- loops of edges,
- shells of faces,
- nonmanifold adjacancies.
- This is tricky to get right.
- The explicit volume is not needed for computing mass properties.
- The set of the vertices with their neighborhoods suffices.
Volume Determination

- Box:
- V =
 i
si xi yi zi
i
si xi yi zi
- si: +1 or -1
- General rectilinear polygons:
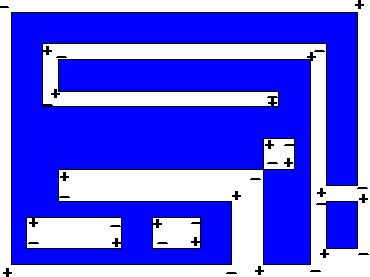
- 8 types of vertices, based on neighborhood
- 4 are
type "+", 4 "-"
- Area =
 (sixiyi)
(sixiyi)
- Perimeter =
 (+xi+yi)
(+xi+yi)
Rectilinear Polyhedron Volume
- V =
 i
si xi yi zi
i
si xi yi zi
- 2 classes of vertices: s i = +1 , or -1.
- Extends to lower dimensional properties, like area and edge length.
- Extends to general polyhedra.
Vertex Classes
- Each vertex has 8 adjacent octants.
- Each octant is either interior or exterior to the polyhedron.
- Which octants are interior determines the vertex's sign.
- Debugging this was tricky.
Properties
The output union polyhedron will be represented as a set of
vertices with their neighborhoods.
- no explicit edges; no edge loops
- no explicit faces; no face shells
- no component containment info
- represents general polygons: multiple nested or separate comps
- any mass property determinable in one pass thru the set
- parallelizable
- amenable to external storage implementation, if necessary.
Volume Computation Overview
- Find all the vertices of the output object.
- For each vertex, find its location and local geometry.
- Sum over the vertices, applying the formula.

Finding the Vertices
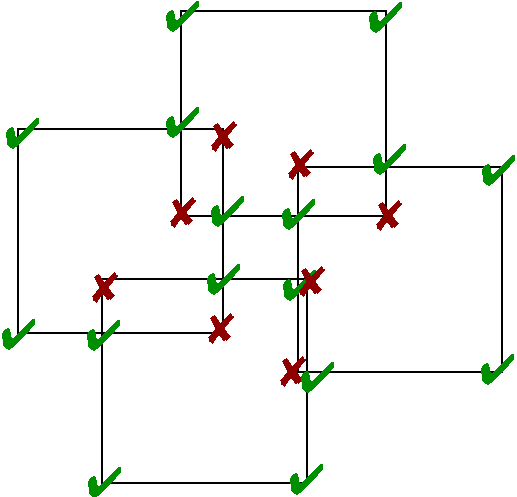
3 types of output vertex:
- vertex of input cube
- intersection of edge of one cube with face of another,
- intersection of three faces of different cubes.
Find possible output vertices, and filter them
An output vertex must not be contained in any input cube.
Isn't intersecting all triples of faces, then testing each candidate output vertex against every input cube too slow? No, if we do it right.
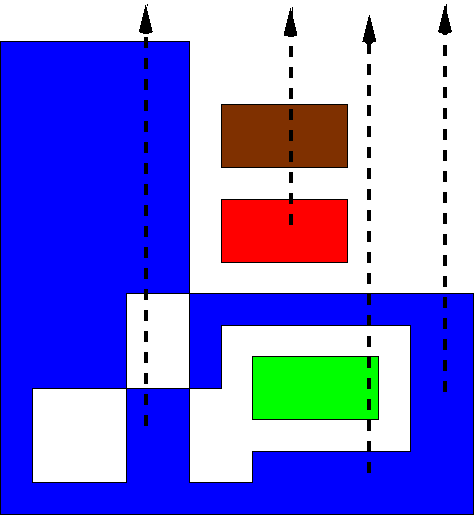
Use a 3D Grid - Summary
- Overlay a uniform 3D grid on the universe.
- For each input primitive (cube, face, edge), find which cells it overlaps.
- With each cell, store the set of overlapping primitives.
Grid - Properties:
- Simple, sparse, uses little memory if well programmed.
- Parallelizable.
- Robust against moderate data nonuniformities.
- Bad worst-case performance: could be defeated be extremely nonuniform data.
- Ditto any hierarchical method like an octree.
Advantage of the Grid
- Intersecting primitives must occupy the same cell.
- The grid filters the set of possible intersections.
Covered Cell Concept
- Only visible intersections contribute to the output.
- That's often a small fraction - inefficient.
- Solution: add the cubes themselves to the grid.
Adding the Cubes Themselves to the Grid
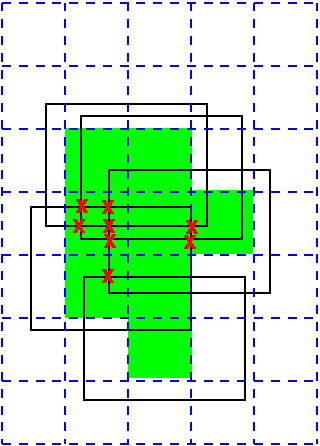
- For each cubes, find which cells it completely covers.
- If a cell is completely covered by a cube, then nothing in
that cube can contribute to the output.
- Find the covered cells first.
- Do not insert any objects into the covered cells.
- Intersect pairs and triples of objects in the noncovered
cells.
If the cell size is somewhat smaller than the edge size then
almost all the hidden intersections are never found. Good.
Expected time =  (size(input) + size(useful intersections)).
(size(input) + size(useful intersections)).
Filter Possible Intersections
by superimposing a uniform grid on the scene.
- For each input primitive (cube, face, edge), find which cells it overlaps.
- With each cell, store the set of overlapping primitives.
- Expected time =
 (size(input) + size(useful intersections)).
(size(input) + size(useful intersections)).
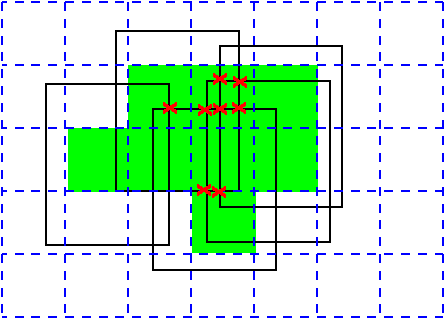
Uniform Grid Qualities
Major disadvantage: It's so simple that it apparently cannot work,
especially for nonuniform data.
Major advantage: For the operations I want to do
(intersection, containment, etc), it works very well for any real
data I've ever tried.
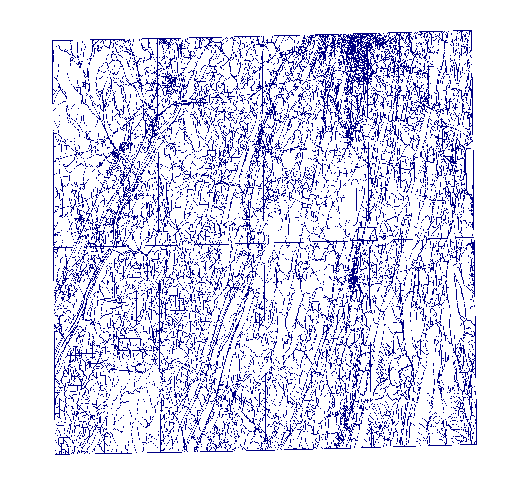
USGS Digital Line Graph
| 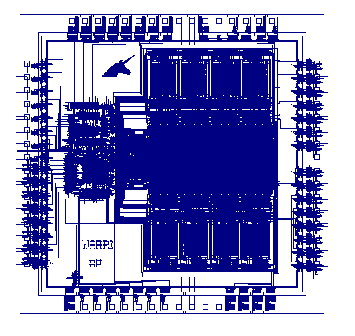
VLSI Design
| 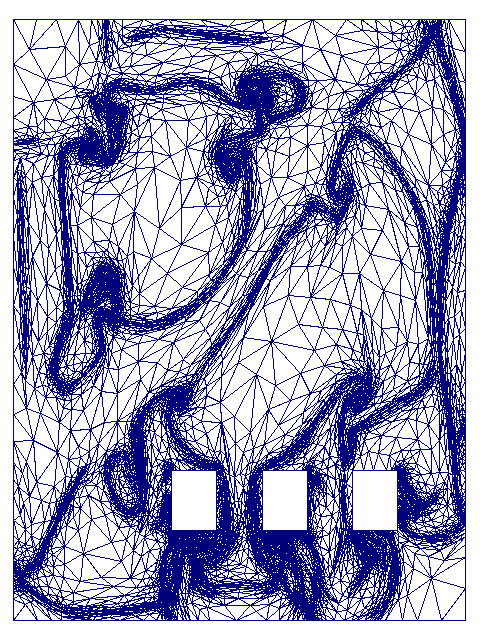
Mesh
|
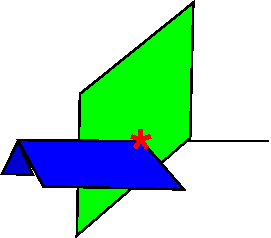
Face-Face Intersection Details
- Iterate over the grid cells.
- In each cell, test all triples of faces, where each face
must be from a different cube, for intersection.
- Three faces intersect if their planes intersect, and the
intersection is inside each face (2D point containment).
- If the 3 faces intersect, look up si
in a table and add a term to the accumulating volume.
- The implementation is easier for cubes.
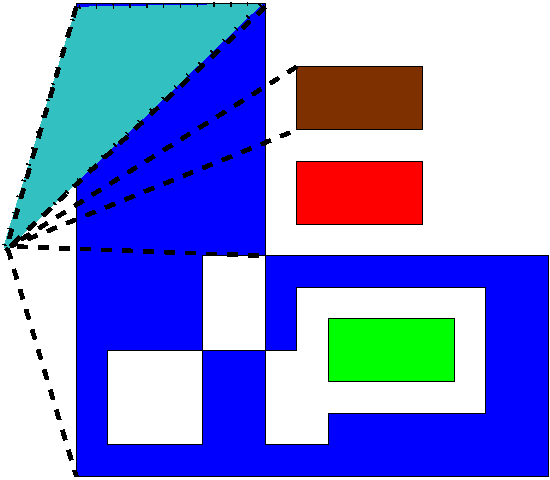
Point Containment Testing
P is a possible vertex of the output union polyhedron.
Q: Is point P contained in any input cube?
A:
- Find which cell, C, contains P.
- If C is completely covered by some cube then
P is inside the covering cube.
- Otherwise, test P against all the cubes that overlap C.
The expected number of such cubes is constant, under broad conditions.
Simulation of Simplicity
- We must resolve degeneracies.
- For any equality, break the tie by comparing the cubes' ID numbers.
- However, now lower-dimensional mass properties give different results than for a regularized set operation.
- E.g., if two cubes abut on a face, then either both faces or neither face are included.
- That is topologically valid.
Execution Time
- N: number of cubes
- L: edge length, in a 1x1x1 universe.
- Expected number of 3-face intersections =
 (N3 L6)
(N3 L6)
Effect of Grid
- Good choice of cell size: half the cube size.
- G: number of grid cells on a side = 2/L.
- Number of face triples: N3
- Prob. of a 3-face test succeeding = N-2L6.
- Depending on asymptotic behavior of L(N), this tends to 0.
- With the grid, prob. of 3 tested faces actually intersecting = c,
independent of N and L(N) .
- Big improvement!
Effect of Covered Cells
- Expected number of 3-face intersections =
 (N3L6)
(N3L6)
- However, for uniform i.i.d. input, expected number of
visible intersections =
 (N).
(N).
- With covered cells, probability that a computed
intersection that is visible = c, independent of
N and L(N) .
- Big improvement!
- Time to test if a point is inside any cube is also constant.
- Total time reduces to
 (N) .
(N) .
Limitations
- If the scene's depth is very large, and cubes are
constrained to be completely inside the universe:
- Then all the interior cells, but none of the border cells
are covered.
- This nonuniformity increases the time.
- If L is small, then proportionally small cells
take too much memory.
- However, actually, there is a broad range of reasonable G.

Parallel Implementation
- Pentium-class processors allow only 3GiB memory per user process.
- Machine may have 12GiB real memory, so real memory > virtual memory!
- Solution: decompose problem into pieces and process in parallel.
- Cannot just slice up the input: this increases the area and edge length.
- Observation: inserting objects into cells is quicker than
testing the cells for intersections.
- Solution:
- Insert the {cubes, faces, edges} into the cells.
- Dustribute the cells among the processors, and test for
intersections in parallel.
- Each process reads several GiB of data, but writes only 3 words:
its part of the volume, area, length.
Implementation
- Very compact data structures.
- Random (Tausworth generator) uniform i.i.d. cubes.
- 1000 executable lines of C++.
- dual 2.4GHz Xeon with 4GiB memory, Linux.
Small Datasets are Fast
- 10,000 cubes; 0.03 edge length
- 60x60x60 grid
- Not using parallelism
- Execution time: 2.5 CPU secs
- Memory: 15 MB.
Large Datasets are Feasible
- 20,000,000 cubes
- 0.009 edge length (quite small, few intersections).
- 500x500x500 grid
- Using 4 parallel processes.
- Execution time: 2000 to 2200 CPU secs per process. I.e.,
the work was evenly divided.
- Memory per process: 2.6 GB
Why not larger datasets? Address space limitations.
Creating more parallel processes thrashes the memory. We're
creating separate sequential processes, but still working on
the interfacing.
Implementation Validation
-
- The terms summed for the volume are large and mostly cancel.
- Errors would be unlikely to total to a number in [0,1].
-
- The expected volume is 1-(1-L3)N.
- Compare to computed volume.
- Assume that coincidental equivalence is unlikely.
-
- Construct specific, maybe degenerate, examples with known volume.
Data Validity Test
These formulae require consistent data.
Use that property to validate the input data consistency:
- Randomly rigidly transform the polyhedron.
- If the computed mass properties change, the data is inconsistent.
- Otherwise, repeat.
Real Datasets are Nonuniform!
-
Maybe we should subdivide the grid adaptively? Obvious, but wrong!
- The algorithm is very robust. Varying edge lengths are not a problem.
- Here are two datasets previously tested for edge intersection.
- Note how nonuniform they are.

USGS Digital Line Graph
| 
VLSI Design (J Guilford)
| 
Mesh (M Shephard)
|
Extension to General Polygons

The only data type is the incidence of an edge and a vertex, and
its neighborhood. For each such:
- V = coord of vertex
- T = unit tangent vector along the edge
- N = unit vector normal to T pointing into the polygon.
Polygon: {(V, T, N)} (2 tuples per vertex)
Perimeter = - (V.T).
(V.T).
Area = 1/2  ( V.T V.N )
( V.T V.N )
Multiple nested components are ok.
Extension to 3D
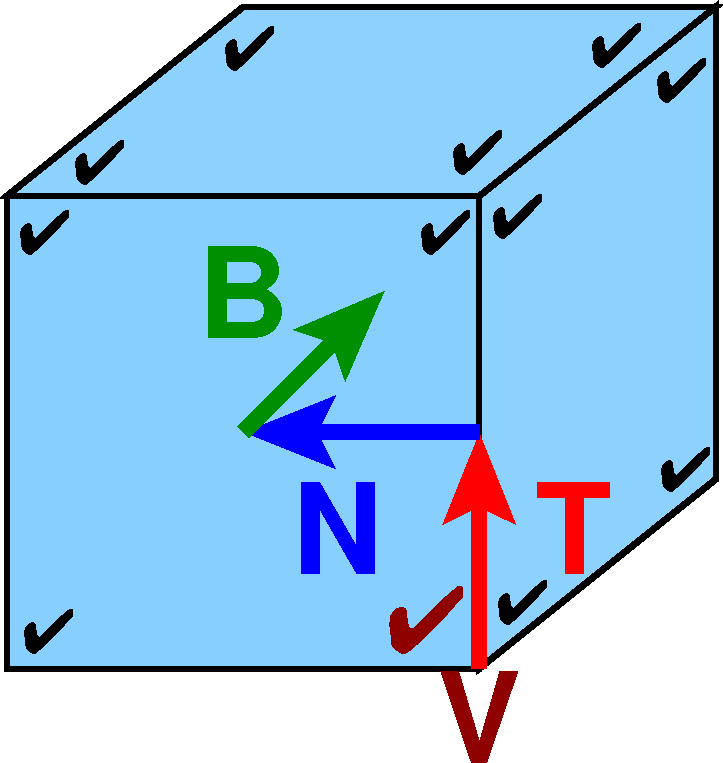
The only data type is the incidence of a face, an edge and a vertex, and
its neighborhood. For each such:
- V = coord of vertex
- T = unit tangent vector along the edge
- N = unit vector normal to T in the plane of the face, pointing into the face.
- B = unit vector normal to T and N, pointing into the polyhedron.
Polyhedron: {(V, T, N, B)}
Perimeter = -1/2  (V.T)
(V.T)
Area = 1/2  ( V.T V.N )
( V.T V.N )
Volume = -1/6  ( V.T V.N V.B )
( V.T V.N V.B )
Intersection Volumes from Overlaying 3-D Triangulations
Existing 2-D implementation: overlay two planar graphs;
find areas of all intersection regions.
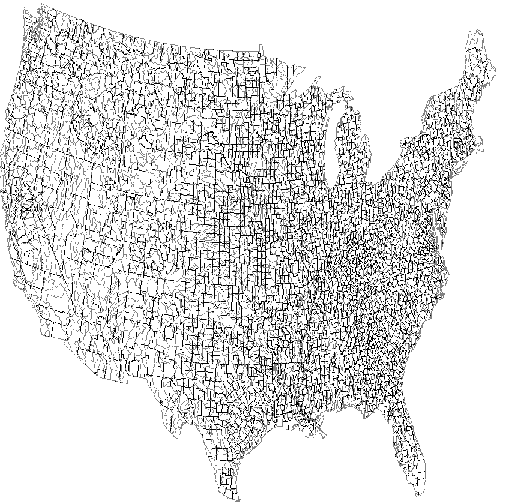
E.g. overlay counties of the coterminous US against hydrography
polygons. Map stats:
Map #0: 55068 vertices, 46116 edges, 2985 polygons
Map #1: 76215 vertices, 69835 edges, 2075 polygons
Total time (excluding I/O): 1.58 CPU seconds.
Future: Extend to 3-D.
Application: Interpolate some property from one triangulation to the other.
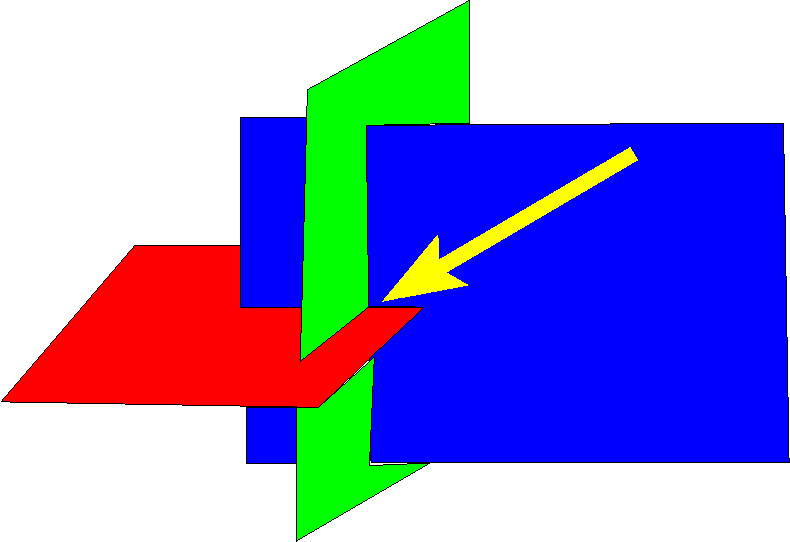
Extension: More Complicated Boolean Operations
Given a red object defined as the union of many overlapping
cubes, and a similar blue one.
- Do they intersect?
- Simplified to 2-D: N red edge segments, and N blue ones.
- There may be O(N2) red-red and blue-blue intersections.
- You don't know them.
- There are O(1) red-blue intersections.
- Find them.
- No subquadratic worst-case algorithm (SFAIK).
Moral: sometimes heuristics are necessary.
Other Possible Extensions
- Online algorithm, with incremental input insertions, would be easy.
- Online deletion of cubes should be only a little harder, if
covered cells not used.
- This could be fast enough to be process hundreds of cubes at
video update rates (1/30 sec).
Summary
Guiding principles:
- Use minimal possible topology, and compact data structures.
- Short circuit the evaluation of volume(union(cubes)).
- Design
for expected, not worst, case input.
- External data structures unnecessary, tho possible.
Allows very large datasets to be processed quickly in 3-D with
algorithms where sweep lines might have problems.
A paper on this subject is at http://wrfranklin.org/research/union3/union3.pdf.
The html version of this talk is on my website http://wrfranklin.org/Research/geo_ops_millions-jul2004/
. It is designed to be displayed in full screen mode with Opera.
Thanks!
Portions of this material are based upon work supported by
the National Science Foundation
under Grants ENG-7908139, ECS-8021504, ECS-8351942,
CCF-9102553, and CCF-0306502, and by IBM, Sun Microsystems,
and Schlumberger--Doll Research.
Dr. Wm Randolph Franklin,
Email: wrfATecse.rpi.edu
http://wrfranklin.org/
☎ +1 (518) 276-6077; Fax: 6261
ECSE Dept., 6026 JEC, Rensselaer Polytechnic Inst, Troy NY, 12180 USA
(GPG and PGP keys available)
Copyright © 1994-2003, Wm. Randolph Franklin.
You may use my material for non-profit research and education,
provided that you credit me, and link back to my home
page.





 (V.T).
(V.T).



 (P lg P) .
(P lg P) .